Overturn Moment FOS when Uplift is involved.

[StrEng007]

When checking the overturn factor of safety provided in Enercalc vs. the method used in “Foundation and Anchor Design Guide for Metal Building Systems” by Alexander Newman, I found some discrepancies. Rotation is considered around point A.

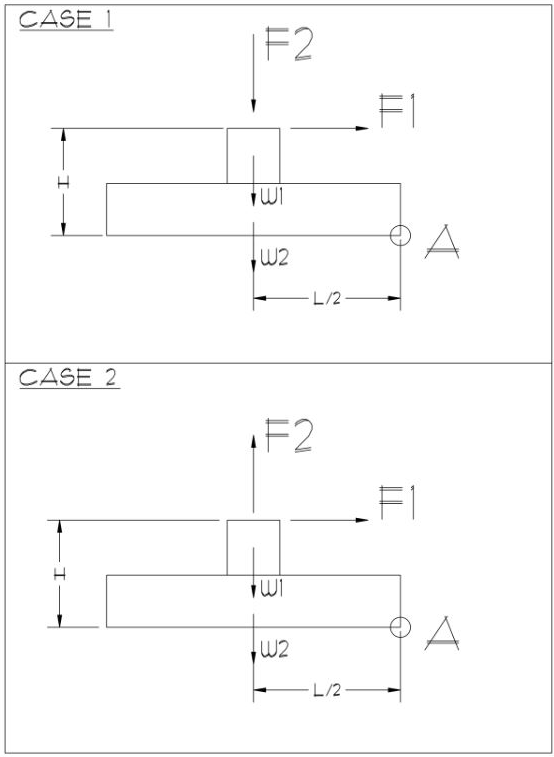
Enercalc, Case 1:
Resisting Moment, Mres = L/2*(F2+w1+w2)
Applied OT Moment, Mot = F1*H

Enercalc, Case 2:
Resisting Moment, Mres = L/2*(w1+w2)
Applied OT Moment, Mot = (F1*H)+(F2*L/2)

-------------------------------------------------------------

Text Ref., Case 1: (Same as Enercalc)
Resisting Moment, Mres = L/2*(F2+w1+w2)
Applied OT Moment, Mot = F1*H

Text Ref., Case 2:
Resisting Moment, Mres = L/2*(w1+w2-F2)
Applied OT Moment, Mot = (F1*H)

My biggest concern is from Case 2. Each method gives different answers and will provide a different factor of safety against overturning. This isn’t covered in any references I have for retaining walls since we don’t typically have uplift loads on them. For any of you who do PEMBs, what do you use?

I know some of you might comment that the load directions wouldn’t make sense for typical PEMB reactions. My question is more to do with calculating the overturning and resisting moments, so don’t get mixed up about load directions.

 

[jayrod12]

Look at the algebra, those are equivalent. They should produce exactly the same answer.

 

[WinelandV]

If you're looking at the net moment (Mres - Mnet), then yes, they are equivalent. However, when calculating a FOS, they are not the same. For Case 2, the Text Ref would indicate a much higher FOS than from Enercalc.

My opinion is that Enercalc is doing the check appropriately.

 

[jayrod12]

I design in the LRFD world where we don't use FOS anymore. We just check capacity against demand. So I see your point, and agree that whichever is the most conservative is the proper way to go.

 

[StrEng007]

Jayrod,
The applied OT moment and the resisting moment as evaluated above are not equivalent for both cases, neither is the FOS... but yes, the net moment will be the same.

Winelandv,
I agree with your conservative approach. Have you seen this discussed anywhere?

 

[WinelandV]

This is a good one. Look for JoshPlum's comment near the bottom.

thread507-343140

 

[Lomarandil]

I've had this debate before (deadman with a pipe/cable brace in tension).

I think physically, the text reference's method is more representative of what happens and the practical FOS.

However, the overturning FOS is typically defined as the sum of resisting moments divided by the sum of overturning moments, so Enercalc's method is technically correct per our engineering convention.

Assuming you're checking the FOS against the conventional limit of 1.5, you should probably follow the conventional definition.

 

[canwesteng]

The Enercalc method is correct. For FOS calculations, it should be resisting forces over the forces causing overturning - F2 is a force causing overturning and must be counted with OT moment.

 

[StrEng007]

Correct me if I'm wrong, but the whole FOS check for overturn moment seems kind of arbitrary. The FOS check is entirely separate from the actual distribution of forces under a footing. Consider the fact that a single uplift load, concentric to the footing will not induce any overturn reactions as it will be aligned with the centroid of the footing (ie, only concentric footing dead load and concentric footing uplift, no lateral considered). Technically, the only thing it will do is affect the P/A portion of the equation P/A +/- M/S.

However, when you look at it from a point of view of the "Enercalc" method, this uplift is indeed an applied overturning moment.

This means that that we're considering the force distribution of the heel (or toe) as a single tipping point of infinite compression resistance, which I don't entirely agree with. In reality, we're going to have distributed compression force acting to resist overturn. Is the FOS check an old off the cuff check from the past?

 

[JoshPlumSE]

This is indeed an issue that we ran into when working on the RISAFoot program. And, therefore, an issue I have discussed with multiple engineers over the years.

I tend not to label the methods as "incorrect" vs "correct". Rather I tend to refer to them as a "Traditional / Simplistic" method vs a "true safety factor" method.

Now, it should be clear that I prefer what I call "true safety factor" method.

If anyone is interested, below is a link to write-up in the RISAFoot help file which explains how that program works (which appears to be similar to Enercalc) and compares the results of the two methods.

http://risa.com/risahelp/risafoot/Content/Stabilty and Overturning.htm

 

[JStephen]

If you have a single force and a single strength, then the calculation of a factor of safety is intuitive and simple. Where you have multiple forces and multiple effects that can result in failure, the term "factor of safety" isn't so meaningful. You can arbitrarily define it, but then again, you can arbitrarily define it in different ways, too, and that seems to be the issue above.

Note that failure could be by vertical uplift as noted above, could be taken as a loss of contact on the light side, could be taken as excessive bearing on the heavy side, etc.