PE Civil-Struct Practice Problem 1

[larcix]

I'm working on studying for my PE, but one of my practice exam questions is confusing me, even with the answer worked in the back. I think they forgot to multiple by 2, which is pretty bad for a reference practice exam. Maybe you can direct me to my mistake:

Here is the question (its only a text question):
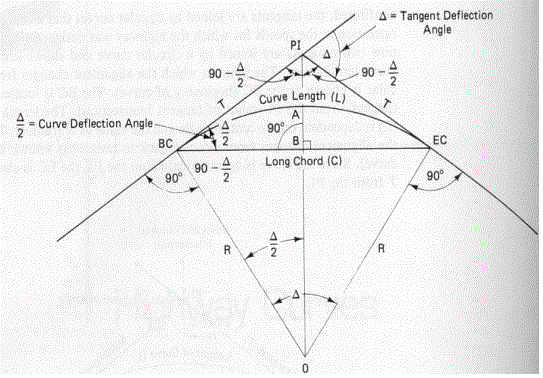
For a new horizontal curve with the following givens:
Station at PI = 12+40.00
Degree of curve = 10°
Deflection angle = 12°30'
Question: What's the station at PT?

I understand that the station is just 1240', and the Degree of Curvature, D, is the degree the curve sweeps over a chord/arc length of 100'. I also found online (and was able to convince myself this was correct) that the Deflection Angle is equal to the intersection angle divided by 2, the intersection angle being the total angle the curve must sweep from PC to PT, so the answer is basically just:

Length of curve = [Total sweep angle]/[sweep angle per 100'] = 2*[Deflection Angle]/[degree of curve] * 100' = (2*12.5/10)*100' = 250'
Station PC = PI - L/2 = 1240 - 250/2 = 1115
Station PT = PC + L = 1115 + 250 = 1365'
The final answer is 13+65.00

The available options are 12+80, 13+2, or 13+65. The answer in the back doesn't multiple the Delfection Angle by 2, gets a curve lenght of 125' and the station at 13+2. Based on everything I can find, that's wrong.

 

[Ingenuity]

It has been 40 years since I did horizontal curve calcs (first year at uni), so bear with me on the following, as I am using first principles, not 'canned' formulas:

Degree of curvature, D, (defined as angle over an arc length of 100') is given as 10[sup]o[/sup], so using arc length = R D = 100' , and re-arranging will give you R (but must have angle in radians) so R = 100'/(10[sup]o[/sup] Π /180) = 572.958'

Define deflection angle as Δ = 12.5[sup]o[/sup]

Calc T, tangent length: T = R tan(Δ/2) = 572.958*tan(6.25) = 62.75'

Station at PC = PI - T = 1240.0 - 62.75 = 11+77.25'

Arc length of horizontal curve, α = R Δ (with Δ in radians) so α = 572.958*(12.5*Π/180) = 125.00'

So Station PT = 11+77.25 + 125.00 = 13+02.25
​

So I agree with curve length of 125' and the station of the PT.

The deflection angle is equal to the intersection angle (Δ, above), if we are referring to the nomenclature correctly.

 

[Settingsun]

Jargon just to confuse people and cause errors. Throw it in the bin and start again.

This site has "tangent deflection angle" and "curve deflection angle" which differ by a factor of two. You only have "deflection angle"... That said, presumably tangent deflection angle is the main one since it gets a symbol.

https://www.cpp.edu/~hturner/ce220/circular_curves.pdf

 

[Ingenuity]

Following from steveh49 comments above, I have never heard of "degree of curve", defined as angle over a fixed arc length of 100'. Maybe it is a US or North American thing.

...and after Googling "degree of angle", it appears to be defined as EITHER chord length of 100' or arc length of 100'. Now that is confusing! Which is it. Just give us the R and be done with all the jargon!

 

[dik]

Memories really fuzzy on this... I think the degree of curve establishes the radius of the curve and the deflection angle is the angle between the straight line segments of the road.

Rather than think climate change and the corona virus as science, think of it as the wrath of God. Feel any better?

-Dik

 

[Settingsun]

We don't do these exams in Australia but I read about them on here. Definite flavour of proving you could have been an engineer in the 1950s.

This 100' thing sounds as though a 100' chain was lugged around back in the day. Computers do all of this now. Surveyors show up on site with the 3d model loaded into their gadgets and gps positioning.

 

[larcix]

This all just seems to be a large terminology misunderstanding. Based on steveh49's image, I would say that 12.5° is the TANGENT angle (as it's the one with a symbol given). But I found multiple references, this one being the most clear (

https://wsdot.wa.gov/publications/manuals/fulltext/M22-97/Chapter11.pdf

) that specifically states the DEFLECTION ANGLE (DC) is the angle for the full curve from the point PT or PC (which is half the DELTA or the TOTAL INTERSECTION ANGLE, aka Δ/2), while the typical use for DELFECTION ANGLEs (dc, lowercase) is for the angle between tangents at any given points on the curve, the DC being the maximum possible dc.

Based on this terminology, I would multiple the 12.5° by 2 to get the full intersection angle.

Thanks for all the help, guys. I'll just need to hope they don't try and get tricky with their curve terminology on the actual test.