Hello,
I hope there is someone who can help me with the problem I am trying to solve. I have a structure composed of a beam, located at the centre and connected to two plates. Each plate is supported by a torsional spring. Since the stiffness of the plate is higher than the one of the beam, the plate can be considered as a rigid body. When the plates are loaded with a force "Fe", they rotate downwards due to the torsional springs.
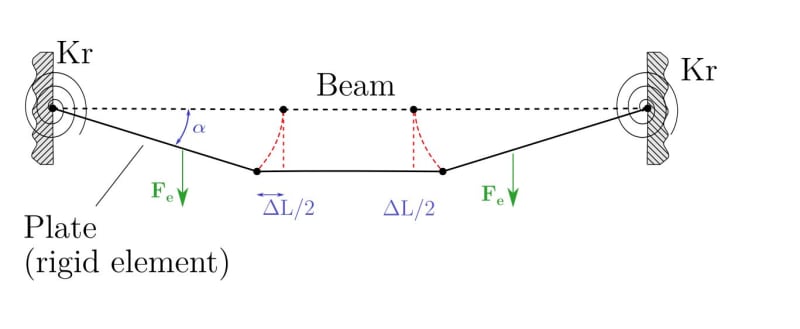
The spring constants and all geometrical parameters are known. In particular:
a= distance between the point of application of the force and the torsional spring;
b= plate length;
c= beam length;
Since the structure is hyperstatic, I have tried to solve using the method of superposition. The redundant reaction forces are the moment at the torsional springs.
The "primary" associated isostatic structure is:
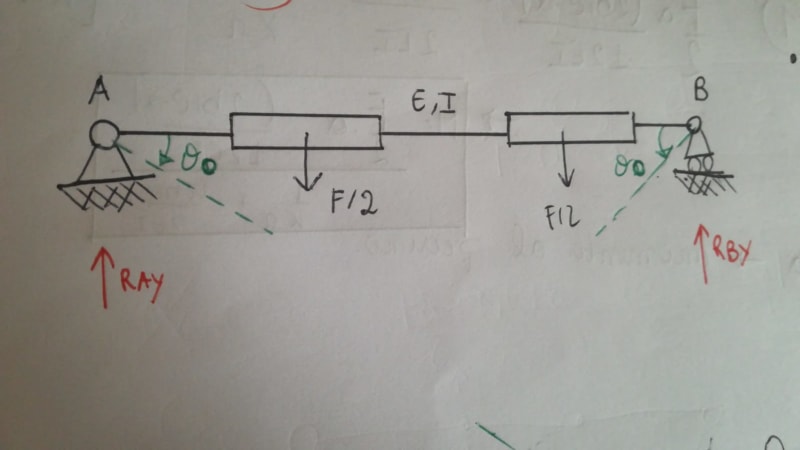
where the rotation (computed using the known solutions for beams) is:
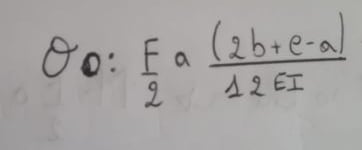
Then, I computed the rotation due to the moment of torsional springs:
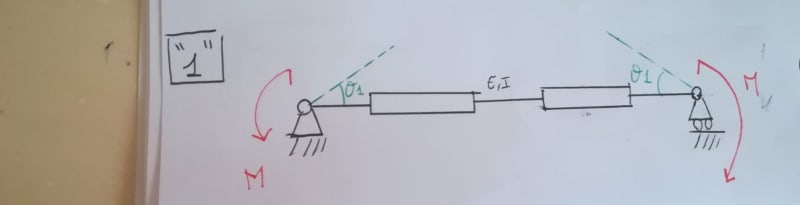
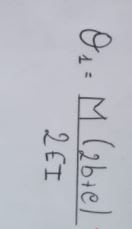
For the torsional spring:

I compute the moment M from the compatibility equation:
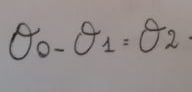
If the moment M is known, solve the structure is easy.
I do not know if this procedure is correct or if I am doing something wrong. Thank you for your time and help.
Kindest,
Chi
I hope there is someone who can help me with the problem I am trying to solve. I have a structure composed of a beam, located at the centre and connected to two plates. Each plate is supported by a torsional spring. Since the stiffness of the plate is higher than the one of the beam, the plate can be considered as a rigid body. When the plates are loaded with a force "Fe", they rotate downwards due to the torsional springs.

The spring constants and all geometrical parameters are known. In particular:
a= distance between the point of application of the force and the torsional spring;
b= plate length;
c= beam length;
Since the structure is hyperstatic, I have tried to solve using the method of superposition. The redundant reaction forces are the moment at the torsional springs.
The "primary" associated isostatic structure is:

where the rotation (computed using the known solutions for beams) is:
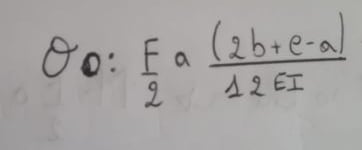
Then, I computed the rotation due to the moment of torsional springs:

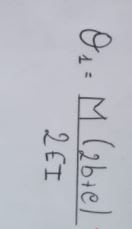
For the torsional spring:

I compute the moment M from the compatibility equation:
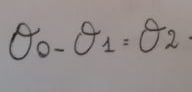
If the moment M is known, solve the structure is easy.
I do not know if this procedure is correct or if I am doing something wrong. Thank you for your time and help.
Kindest,
Chi
