Navigation
Install the app
How to install the app on iOS
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
More options
Style variation
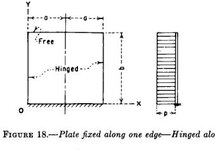
-
Congratulations MintJulep on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Reactions of flat plate pinned on 3 sides 1
- Thread starter danvines
- Start date
- Status
- Not open for further replies.
SWComposites
Aerospace
Hmm, Roark only gives stress and deflection, not the edge reactions. Maybe a FEM?
There might be, but if not, you should be able to zero in on a reasonable answer using your understanding of structures. If the slab dimensions are 'a', 'b' where 'a' is the longer side, it is clear that the free side has zero reaction. If the free side has length 'b', the opposite side has about the same reaction as a b x b plate.I’m at my wits’ end. There’s GOTTA be a “simple” formula or tables for the reactions on a 3-sides pinned, 1-side free rectangular flat plate. I know how to calculate maximum stress and deflection, but I need reactions under a uniform load. Please help.
Alternatively, if you think you know the deflection at all points, then you should be able to determine the reactions using statics.
As a further alternative, simply make a conservative guess, and if the three sided supports are beams, remember that they too deflect.
Last edited:
- Thread starter
- #5
Thanks. I think I just needed to hear someone else say that.I likely have a table somewhere, but realistically can you not just do tributary areas. It's not going to be perfect but it's probably good enough for a pinned condition
GregLocock
Automotive
"Pinned" is doing a lot of work in your question. Do you mean unable to provide anything but vertical forces, or merely unable to apply moments about the axis of the edge?
GregLocock
Automotive
so you've got sides AB BC and CD are SS, and AD is free. If you had a uniform reaction per unit length on the 3 SS sides, then in side view obviously there would be too much force upwards exerted by BC. So the reaction per unit length near A and D must be higher than on BC.
A very crude model suggest that for a square plate the load/m along BC will be 1/6 of that at A, just to get static equilibrium
A very crude model suggest that for a square plate the load/m along BC will be 1/6 of that at A, just to get static equilibrium
Last edited:
I think it will depend on what you need those forces for. I would assume there is some variation, and likely, a reversal of direction, of the loads along the edges. If that's what you need, FEM is likely the simplest solution. You may want to look into Timoshenko's Theory of Plates and Shells, where you may find analytical solutions, but those tend to be infinite double series, etc., so somebody proficient with FEM can likely come up with numbers faster that way.
If you don't need that amount of detail, I would suggest treating the plate as a rigid plate with elastic supports around the edges, and summing moments in both directions plus vertical loading should give you a solution of the forces along each edge.
If I remember correctly, a flat plate simply resting on a simply supported edge on all four sides will actually lift at the corners when loaded. But I don't remember where I've seen that, and may be remembering wrong. Anyway, that behavior would be captured by the first approach and not the second.
Note also that thin plates/ large deflections and/or edges restrained in the plane of the plate would require additional work to analyze.
If you don't need that amount of detail, I would suggest treating the plate as a rigid plate with elastic supports around the edges, and summing moments in both directions plus vertical loading should give you a solution of the forces along each edge.
If I remember correctly, a flat plate simply resting on a simply supported edge on all four sides will actually lift at the corners when loaded. But I don't remember where I've seen that, and may be remembering wrong. Anyway, that behavior would be captured by the first approach and not the second.
Note also that thin plates/ large deflections and/or edges restrained in the plane of the plate would require additional work to analyze.
TRAK.Structural
Structural
There is most certainly a formula for this based on plate/shell theory, but its probably not the simplest formula you've ever seen. If you don't need to be exact than I'd start with looking at tributary areas based on the aspect ratio of the rectangle. More context to your particular scenario may inform what level of accuracy you need to have with this problem.
Did a bit of perusing here:
-For a plate simply supported on all four edges, the corners do indeed lift, and Timoshenko is where I've seen that.
-Timoshenko includes "fixed on 3 edges, free on fourth" but not simply supported on 3 edges/ free on fourth.
-Timoshenko mentions that tables of maximum moment and deflection have generally been calculated by finite difference methods, rather than the series solutions.
-Roark's Formulas for Stress and Strain references a technical paper from 1936 for the simply supported 3 sides/ free one side load case, and that paper is quite likely based on finite differences methods- in which case, there wouldn't be a closed form equation for the reactions.
-For a plate simply supported on all four edges, the corners do indeed lift, and Timoshenko is where I've seen that.
-Timoshenko includes "fixed on 3 edges, free on fourth" but not simply supported on 3 edges/ free on fourth.
-Timoshenko mentions that tables of maximum moment and deflection have generally been calculated by finite difference methods, rather than the series solutions.
-Roark's Formulas for Stress and Strain references a technical paper from 1936 for the simply supported 3 sides/ free one side load case, and that paper is quite likely based on finite differences methods- in which case, there wouldn't be a closed form equation for the reactions.
GregLocock
Automotive
I'm gently working on an FEA model of this, but it might be quicker to cut to the chase and go to an FEA forum and ask there.
-
1
- #13
JoelTXCive
Civil/Environmental
Download Visual Plate by IES Software. It's got about a 5-minute learning curve.
They give you a free 30 day trial.
They give you a free 30 day trial.
- Thread starter
- #14
Thanks everyone. For my case (really high aspect ratio and really thin plate) and the loads involved (pretty small), I decided it would be conservative to simply use tributary areas (full plate height at supported long top edge and 1/2 plate width at supported narrow sides).
can the boundary support in-plane loads (then your thin "plate" will develop membrane loads) ?
when you say "high aspect ratio" do you mean wide (long) and narrow or the other way ? ie is the 4th edge (the one that's free) long or short ?
with a uniform load, I'd consider a 1" wide strip as a SS beam (supported on the two parallel sides).
I think you need to consider membrane action ... if the boundary can't support in-plane loads (to react the in-plane membrane forces) then I think the boundary will feel an enforced displacement (due to the curvature of the panel).
when you say "high aspect ratio" do you mean wide (long) and narrow or the other way ? ie is the 4th edge (the one that's free) long or short ?
with a uniform load, I'd consider a 1" wide strip as a SS beam (supported on the two parallel sides).
I think you need to consider membrane action ... if the boundary can't support in-plane loads (to react the in-plane membrane forces) then I think the boundary will feel an enforced displacement (due to the curvature of the panel).
- Status
- Not open for further replies.
Similar threads
- Replies
- 24
- Views
- 7K
- Question
- Replies
- 3
- Views
- 751
- Replies
- 4
- Views
- 3K
- Locked
- Question
- Replies
- 10
- Views
- 739
- Question
- Replies
- 6
- Views
- 3K