Celt83
Structural
- Sep 4, 2007
- 2,083
Is anyone aware of any worked examples for the computations of Equivalent Nodal Forces for partial loading normal to a shell element?
I have a few of the books noted in the FAQ here that I have started working through namely:
Zienkiewicz - Volumes 1 and 2
Finite element procedures by K J Bathe
A First Course in the Finite Element Method by Daryl L Logan
Programming the Finite Element Method by Smith and Griffiths
I admittedly need to work on my calculus so don't have a full grasp yet on the body and traction force integrals, but none of the books appeared to directly address loadings of this type and in general don't provide many examples for the equivalent nodal forces.
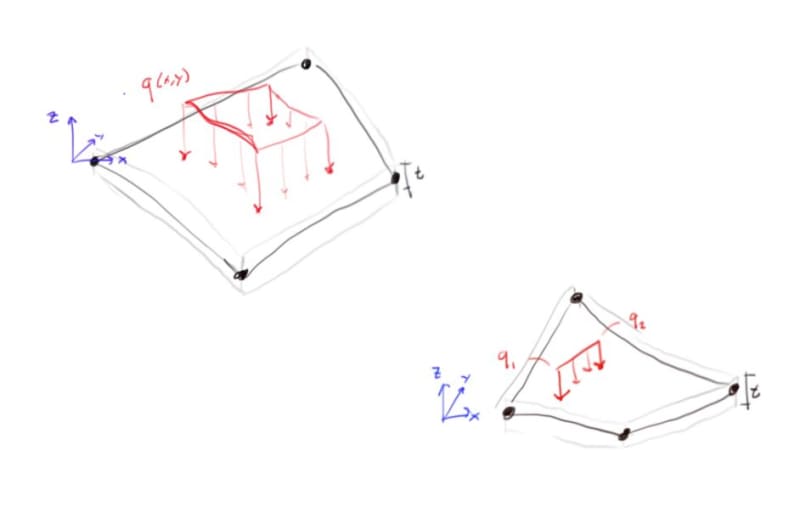
A secondary question is for the body and traction force integrals are these typically done based on the actual element geometry or the isoperimetric formulation? Seems you could use the isoperimetric shape functions and jacobian and just need to work out the load function change of variable from x,y to eta,xi (for many cases this would appear to be a direct substitution).
I'm making a thing: (It's no Kootware and it will probably break but it's alive!)
I have a few of the books noted in the FAQ here that I have started working through namely:
Zienkiewicz - Volumes 1 and 2
Finite element procedures by K J Bathe
A First Course in the Finite Element Method by Daryl L Logan
Programming the Finite Element Method by Smith and Griffiths
I admittedly need to work on my calculus so don't have a full grasp yet on the body and traction force integrals, but none of the books appeared to directly address loadings of this type and in general don't provide many examples for the equivalent nodal forces.

A secondary question is for the body and traction force integrals are these typically done based on the actual element geometry or the isoperimetric formulation? Seems you could use the isoperimetric shape functions and jacobian and just need to work out the load function change of variable from x,y to eta,xi (for many cases this would appear to be a direct substitution).
I'm making a thing: (It's no Kootware and it will probably break but it's alive!)
