Settingsun
Structural
- Aug 25, 2013
- 1,513
The image below shows the relationship between ultimate rock lateral capacity (p_ur) and rock compressive strength proposed by Reese in his textbook (title shown in the image). The value of rock compressive strength (q_ur) is found from tests on intact specimens, with an adjustment (alpha_r) based on rock quality designation. Lower RQD gives a higher alpha_r.
I would expect lower RQD to give lower p_ur. Do rocks with low RQD have lower intact compressive strength than high-RQD rocks with all else being equal, so that the product of:
[(large) alpha_r] * [(small?) q_ur]
will be lower overall? I think that using intact specimens for the q_ur test would remove the influence of RQD, so that Reese’s formula will give higher lateral capacity for lower RQD.
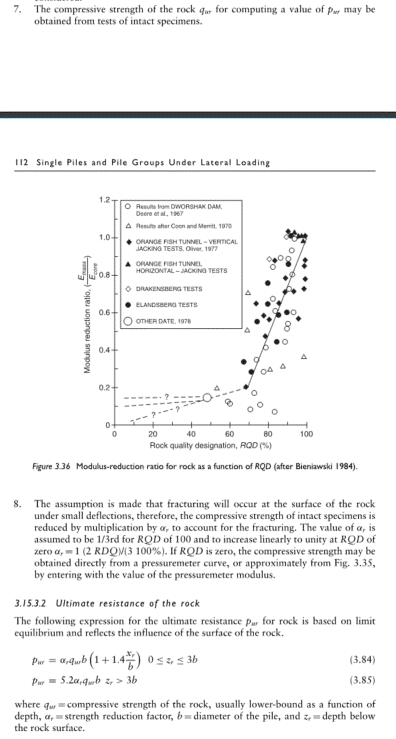
Figure 3.36 in the image shows a relation between RQD and insitu/lab modulus. Bowles says the same relationship applies to insitu/lab compressive strength which supports my understanding, but leaves me thinking the Reese alpha_r factor is counterintuitive and maybe wrong. Note that Reese doesn't suggest reducing q_ur using Figure 3.36.
Comments?
I would expect lower RQD to give lower p_ur. Do rocks with low RQD have lower intact compressive strength than high-RQD rocks with all else being equal, so that the product of:
[(large) alpha_r] * [(small?) q_ur]
will be lower overall? I think that using intact specimens for the q_ur test would remove the influence of RQD, so that Reese’s formula will give higher lateral capacity for lower RQD.
Figure 3.36 in the image shows a relation between RQD and insitu/lab modulus. Bowles says the same relationship applies to insitu/lab compressive strength which supports my understanding, but leaves me thinking the Reese alpha_r factor is counterintuitive and maybe wrong. Note that Reese doesn't suggest reducing q_ur using Figure 3.36.
Comments?

