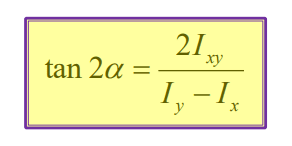Navigation
Install the app
How to install the app on iOS
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
More options
Style variation
-
Congratulations JStephen on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Section modulus of single angle about major/minor principal axis
- Thread starter denguy
- Start date
- Status
- Not open for further replies.
- Thread starter
- #4
Yes, I tried the calculator and was able to find the moment of inertia for the principle axes. However, I'm having a hard time determining the distance as you mentioned.
For the geometric axis: Sx = I/(y-x_c)
How would I find the equivalent distance of (y-x_c) for the principle axes?
For the geometric axis: Sx = I/(y-x_c)
How would I find the equivalent distance of (y-x_c) for the principle axes?
Note, when you work on principal axes, there is no Sx, or Sy, however, there are points of interest, that are measured as the farthest (maximum) and nearest (minimum), or any point, from the principal axes. In order to work on the principal axes, you shall first to break down the force on the geometric axes into component forces aligned with the principal axes, then use superposition to get the maximum/minimum stresses. Review textbook of "Engineering Mechanics" if you forget how to do it.
The sketch below shows the geometric axes (X & Y), the principal axes (1-1 & 2-2), and points of interest (a, b & c), in which the maximum and minimum stress locates.
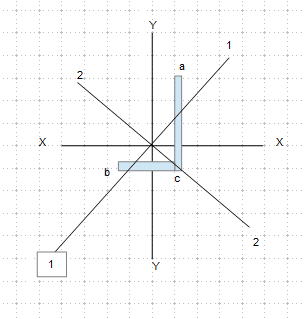
The sketch below shows the geometric axes (X & Y), the principal axes (1-1 & 2-2), and points of interest (a, b & c), in which the maximum and minimum stress locates.

My section properties spreadsheet will calculate the second moment of area about the principal axes for a variety of shapes, and also allows shapes to be rotated and moved, so that the X and Y axes pass through the centroid and are parallel to the principal axes:
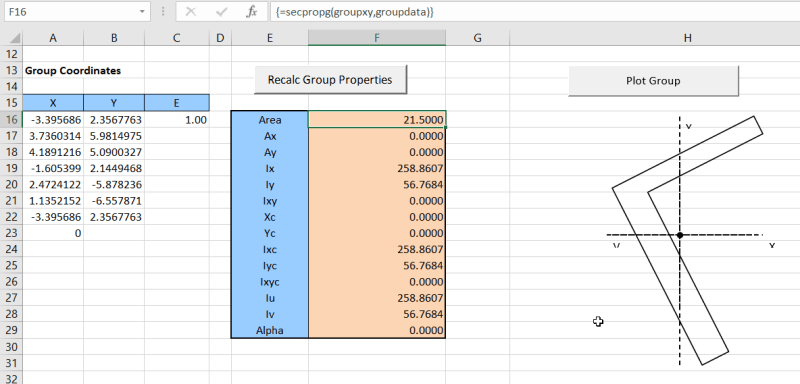
See: for more details and a download link.
Doug Jenkins
Interactive Design Services

See: for more details and a download link.
Doug Jenkins
Interactive Design Services
MikeHalloran
Mechanical
To simplify a bit, angles don't do well in bending.
HSS (hollow structural sections), i.e., round or rectangular steel tubes, do much better.
HSS (hollow structural sections), i.e., round or rectangular steel tubes, do much better.
it's principal.
the minor principal axis of an angle is through the mid-points of the two legs.
the major principal axis is normal and through the corner of the angle.
the intersection of these two is the centroid.
the radius of gyration … I = A*r^2
won't CAD do this for you if you can't do the math ?
The issue is calculating the extreme fiber distance. The principal axes are rotated on the section (as shown above), so calculating the distance is a bit of math. Either do it in CAD, or do it in math …
start with the angle standing upright, set your origin in the corner, determine the co-ords of the ends of the legs; calculate the centroid
this becomes the new origin, re-calculate the co-ords of the ends of the legs; then rotate the axes as calc'd by principal axes
transform the co-ords of the ends of the legs into the rotated (principal) axes.
another day in paradise, or is paradise one day closer ?
the minor principal axis of an angle is through the mid-points of the two legs.
the major principal axis is normal and through the corner of the angle.
the intersection of these two is the centroid.
the radius of gyration … I = A*r^2
won't CAD do this for you if you can't do the math ?
The issue is calculating the extreme fiber distance. The principal axes are rotated on the section (as shown above), so calculating the distance is a bit of math. Either do it in CAD, or do it in math …
start with the angle standing upright, set your origin in the corner, determine the co-ords of the ends of the legs; calculate the centroid
this becomes the new origin, re-calculate the co-ords of the ends of the legs; then rotate the axes as calc'd by principal axes
transform the co-ords of the ends of the legs into the rotated (principal) axes.
another day in paradise, or is paradise one day closer ?
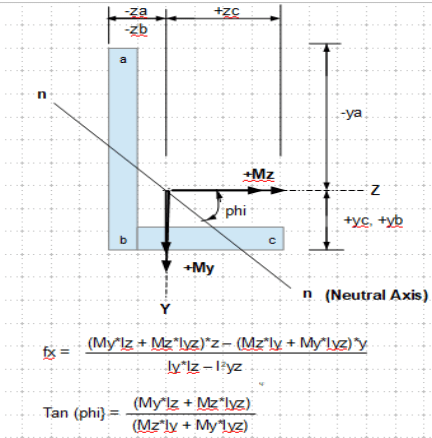
rb said:that may be so, but phi does not depend on the loads.
The equation is copied from "Mechanics of Materials", by Gere and Timodhenko. If one of the moment is zero, it can be reduced to tan(phi) = Iyz/Iy (for My = 0), and tan(phi) = Iz/Iyz (for Mz = 0). The case you referred is a special case - if the principal axes are coincident with the geometric axes, then tan(phi) = y/z = My*Iz/Mz*Iy.
Confusing, isn't it?!
damn ! had a scathing, self-righteous reply 1/2 typed out, really hitting my stride … and then it struck me …
neutral axes … which of course is not a principal axis (but the location of zero stress).
sigh … it was a really good reply !!
another day in paradise, or is paradise one day closer ?
neutral axes … which of course is not a principal axis (but the location of zero stress).
sigh … it was a really good reply !!
another day in paradise, or is paradise one day closer ?
nah … my fault … all the talk of principal axes led me to miss "neutral axis". It would have been more confusing with the principal axes shown (more so since they don't contribute to the solution (only to the obscurity ?).
another day in paradise, or is paradise one day closer ?
another day in paradise, or is paradise one day closer ?
won't CAD do this for you if you can't do the math ?
Sure you can do it in CAD, or in most structural analysis/FEA packages, but I don't know why that is treated as the default approach when it is much easier and quicker to do it in a spreadsheet, which also provides much more convenient access to the results for further analysis.
Doug Jenkins
Interactive Design Services
retired13 said:One question, on the spreadsheet, Ixyc should always be zero, correct?
For the rotated shape, with the XY axes parallel to the principal axes, yes, otherwise no.
One advantage of the spreadsheet, compared to using CAD or FEA, is that the formula for each property is displayed next to the result, so you can check it by hand (and also transfer the formula to other applications).
Doug Jenkins
Interactive Design Services
- Status
- Not open for further replies.
Similar threads
- Replies
- 13
- Views
- 2K
- Replies
- 23
- Views
- 10K
- Replies
- 13
- Views
- 3K
- Locked
- Question
- Replies
- 2
- Views
- 452
- Question
- Replies
- 3
- Views
- 5K