Hey all,
I'm trying to calculate the shear flow to size a weld for a W shape pre-engineered frame. I can't seem to find a procedure to calculate shear flow when the addition of the reinforcing (in my case a WT) lowers the neutral axis below the weld.
In all of the examples I can find, the area in the shear flow equation is described as being the area above the weld. Now I've come to understand that if I am reinforcing the bottom of a beam, it is really the area towards the extreme fiber. However, since the neutral axis is now in the WT reinforcing, I am wondering if the area I need to take for the equation is the area of the existing member (above the weld), or of the WT (below the weld). And subsequently, the distance would be either from lines 2-1 or from lines 3-1 respectively.
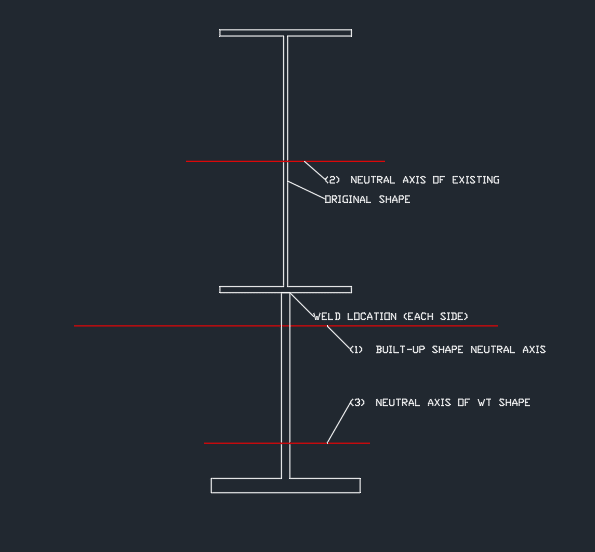
I'm trying to calculate the shear flow to size a weld for a W shape pre-engineered frame. I can't seem to find a procedure to calculate shear flow when the addition of the reinforcing (in my case a WT) lowers the neutral axis below the weld.
In all of the examples I can find, the area in the shear flow equation is described as being the area above the weld. Now I've come to understand that if I am reinforcing the bottom of a beam, it is really the area towards the extreme fiber. However, since the neutral axis is now in the WT reinforcing, I am wondering if the area I need to take for the equation is the area of the existing member (above the weld), or of the WT (below the weld). And subsequently, the distance would be either from lines 2-1 or from lines 3-1 respectively.



