Sizing Exterior Wall Studs with NDS 1

[JackTheEITman]

Hello All,

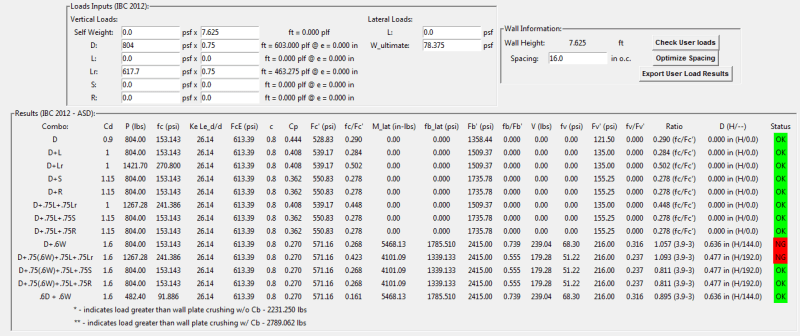
I am having some engineering headaches regarding lining my calculations from the NDS up with some structural software I'm using to check my work. Can I get someone to poke some holes in my hand calculations? I am going nuts trying to figure out what is wrong. Within NDS, equation 3.9-3 keeps coming out with a different number within my software (woodworks Sizer) than it does in my hand calcs.

Assumptions: (1) ply 2x4 Spruce pine fir #2, loaded with 62.7 plf wind after relevant factors (matches loading in software), and 804 lbf dead axial, 617.7 lbf live roof axial. Continuously braced along weak axis.

Wet service factor, Temp factor, incising factor are all 1.

The values I KNOW are correct, because they match the output of my software every time I run it with different values, are for the example's sake:
fb = 1786 psi
Fb' = 2415 psi
fc = 271
Emin = 510,000 psi
Emin' = 510,000 psi
Le1 = 91.5 inches (true column length)
d1 = 3.5 inches
col. stability factor, Cp = .408
Fc = 1150
CF bending = 1.5
CF axial = 1.15

and here are my calculations I'm concerned about - assuming everything above is correct (I will of course go back and double check even those, but want to check the logic below here as well). Could someone point out if anything below is wrong?

Fce1 = .822 * Emin' / (le1/d1)^2 = .822 * 510000 / (91.5/3.5)^2 = 613.4 psi

^This ALONE is putting the second term over the answer woodworks gets, since it is the only unknown I have in the second term of 3.9-3 - so I'm assuming something has to be wrong here? It outputs fb, Fb', and fc identical to my values, and doesn't output Fce.

(the following is wrong, but gave me a correct value: I even tried calculating my own Emin' to see (despite the fact that it outputs Emin' as 510000), taking an assumption that COV=.11 for machine stress rated (help page says it assumes as much), then Emin'=E*[1-1.645*COVe]*1.03/1.66 = 711488. If I also calculate Fc' using a beam stability factor, instead of column stability as I'd assumed, of .946 (taken using Fbe of 4300, Rb = 12), I actually get 1.1! But, it does not work if I change my loads and recheck. Plus, those assumptions are wrong.)

Fc' = Fc * LDF * CF * Cp =
Fc' = 1150 * 1.6 * 1.15 * .408 = 863 psi

Eq. 3.9-3, I'm assuming the third term does not apply since it's not biaxially loaded and would go to zero, which leaves:

(fc/Fc')^2+fb1/(Fb1'(1-(fc/Fce1))) =
(271/863)^2+1786/(2415(1-(271/613.4))) = 1.423

The output from Sizer is 1.10 for equation 3.9-3.

To reiterate, the outputs of my software are in its calculation portion:
fb=1786
F'b=2415
fc=272 (worst case load combo, I agree and got 271)
Emin' = 510000
Cp = .408
And the other ones shown above.

My hunch is that I am applying my factors wrong, but I'm using the factor applicability for sawn lumber chart and I cannot find any errors with the ones I've applied - Sizer appears to multiply following the same convention and yet 3.9-1 keeps coming out incorrrect. Any glaring issues I'm not seeing?

Any input would be greatly appreciated, I'm trying to learn the NDS better.

Thank you!

 

[Celt83]

Is your wind PLF an ultimate or service level value, assuming service level here are the results I get:

Detailed calculations for the axial capacity of a stud with that lateral wind loading (47.025 psf assumed applied to 16" o.c. studs * 0.75 for the load combo):

2x4 (1.50x3.50)- Height:7.625 ft - Species: Spruce-Pine-Fur - Grade: No.1/No.2 - Spacing: 16.0 in

-- Pmax_allow = 1135.62 lbs (851.71 plf)  --
-- PL Crushing (Cb): 2789.06 lbs (2091.80 plf) --
-- PL Crushing (w/o Cb): 2231.25 lbs (1673.44 plf) --

--Common Spacing Capacities--
Axial Capacity at 4" - 6" - 8" - 12" - 16" - 24" spacings:
7.625 ft - 4" O.C. - 2225.92 Lbs (6677.77 plf) - H/767.8
7.625 ft - 6" O.C. - 2007.11 Lbs (4014.22 plf) - H/511.9
7.625 ft - 8" O.C. - 1812.99 Lbs (2719.49 plf) - H/383.9
7.625 ft - 12" O.C. - 1462.79 Lbs (1462.79 plf) - H/255.9
7.625 ft - 16" O.C. - 1135.62 Lbs (851.71 plf) - H/192.0
7.625 ft - 24" O.C. - 473.33 Lbs (236.67 plf) - H/128.0


--Section Properties--
A = 5.250 in^2 -- S = 3.062 in^3 -- I = 5.359 in^4

--Applied Loads--
Pressure: 35.27 psf x Spacing x 1 ft / 12 in = 47.03 plf
Lateral Shear: 179.28 lbs
Lateral Moment: 4101.10 in-lbs
Lateral Delta: 0.477 - H / 192.0

--Stresses--
fc = P/A = 216.308 psi
fv = VQ/Ib = 3V/2bd = 51.224 psi
fb = Mc/I = M/s = 6M/bd^2 = 1339.135 psi
Combined Axial+Bending:
[fc/Fc]'^2 + fb / Fb' [ 1- (fc / FcE)] = 1.000 <= 1.0

--Calculation of Cp--
Fc* = reference compression design value parallel to grain multiplied by all applicable adjusment factors except Cp
Fc* = Fc*Cd*Cm*Ct*Cf*Ci = 1150.00*1.60*1.00*1.00*1.15*1.00 = 2116.00 psi
c = 0.8 - NDS 2005 3.7.1
Ke = 1.0 for both depth and breadth of studs - Ref NDS 2005 appendix G pin top and bottom
Le_b = 12.0 in. - continuously braced by sheathing 12" field nailing assumed
Ke * Le_d / d = 26.143 in < 50
Ke * Le_b / b = 8.000 in < 50
FcE = 0.822 * Emin' / (max[Le_d/d,Le_b/b])^2 - NDS 2005 Section 3.7.1
FcE = 613.389 psi
Cp = ([1 + (FcE / Fc*)] / 2c ) - sqrt[ [1 + (FcE / Fc*) / 2c]^2 - (FcE / Fc*) / c] = 0.270 - NDS 2005 Section 3.7.1

--ASSUMPTIONS--
Design Stud Height = Wall Height inclusive of top and bottom plates
Capacities noted are inclusive of wall self weight - true supporting capacity is (result - panel self weight)
Size Factor_Cf - Wall Studs are visually graded dimensional lumber 2" to 4" North American Species and not Southern Pine
Wet Service Factor_Cm - Wall Studs are visually graded dimensional lumber 2" to 4" North American Species or Southern Pine
Flat Use Factor_Cfu - Wall studs are not loaded on the flat face
Buckling Stiffness Factor_CT - Not Applicable for stud walls
Bearing Area Factor_Cb - Stud greater than 3" from bottom plate end
Beam Stability Factor_CL - Wall studs are continuously sheathed on the compression face
c for Cp calculation based on sawn lumber - NDS 2005 3.7.1
Wall studs are not tapered and not subject to NDS 2005 - 3.7.2

Open Source Structural Applications:

https://github.com/buddyd16/Structural-Engineering

 

[Celt83]

It looks like you calculated Cp based on the Cd=1.0 for just the D+Lr load case, Cd would be 1.6 for the load case including wind pressure which cuts Cp about in half.

Open Source Structural Applications:

https://github.com/buddyd16/Structural-Engineering