gmannix1000
Structural
Hi All,
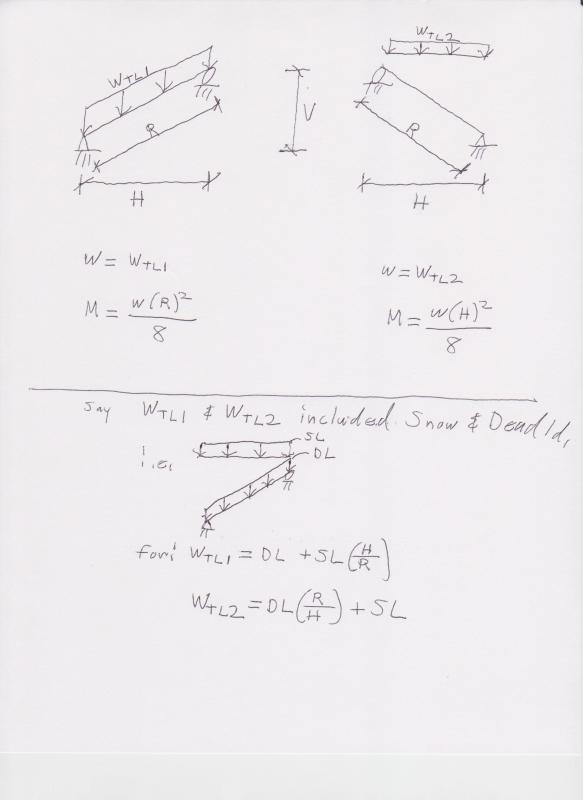
Simple question - roof beam sloping and I just want to double check that I'm calculating the shear, moment and axial loads in the member correctly. See attached for formulae that I am arriving at.
Obviously, let's say the snow and the dead load of the member will act vertically so the UDL on the beam will be wCos(a), with (a) being the angle of the beam. Thus, the axial component of this will be wSin(a), then times the length of the beam, correct?
Also, if this becomes a two span beam, I'd imagine the axial force formula wouldn't change, just the moment and shear formulae?
Is this the correct way of analysing this?
Thanks so much, working myself into a tizzy over this, needlessly no doubt!
Simple question - roof beam sloping and I just want to double check that I'm calculating the shear, moment and axial loads in the member correctly. See attached for formulae that I am arriving at.
Obviously, let's say the snow and the dead load of the member will act vertically so the UDL on the beam will be wCos(a), with (a) being the angle of the beam. Thus, the axial component of this will be wSin(a), then times the length of the beam, correct?
Also, if this becomes a two span beam, I'd imagine the axial force formula wouldn't change, just the moment and shear formulae?
Is this the correct way of analysing this?
Thanks so much, working myself into a tizzy over this, needlessly no doubt!