What is your approach to determining the factor of safety and the overall bearing stress for a spread footing subjected to overturning & uplift loads?
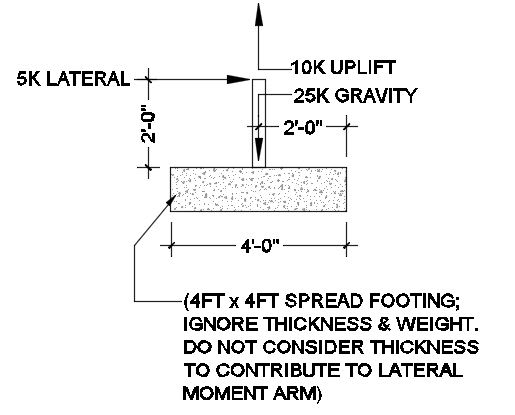
Overturning Factor of Safety Check
Resisting Moment = 25k (2ft) = 50 k-ft
Destabilizing Moment = 5k (2ft) + 10k (2ft) = 30 k-ft
Overturning Moment FOS = 50 k-ft/ 30 k-ft = 1.67
Now, if you consider the resultant load eccentricity and the relationship, Overturn Factor of Safety = L/2e (where L if the footing length, 4ft):
e' = 4ft - (50k-ft - 30k-ft)/25k = 3.2 ft
Eccentricity, e = 3.2ft - 4ft/2 = 1.2 ft
Overturn FOS = L/2e = 4ft/(2 x 1.2ft) = 1.67, OK
When I calculate the bearing stress, my approach is, qmax = (2 x 25k) / [(3 x 4ft)(4ft/2 - 1.2ft)] = 5.20 KSF
However, if you enter the same criteria in Enercalc, you get approx. 1.875 KSF, achieved by:
e' = 4ft - (50k-ft - 30k-ft)/(25k - 10k) = 2.67 ft
Eccentricity, e = 2.67ft - 4ft/2 = 0.667 ft
Overturn FOS = L/2e = 4ft/(2 x 0.667ft) = 3.0, DOES NOT EQUAL 1.67
qmax = [2 x (25k-10k)] / [(3 x 4ft)(4ft/2 - 0.667ft)] = 1.875 KSF
My question is, what is the best way to handle the destabilizing uplift load? And why does Enercalc's method not maintain the relationship where OT FOS = L/2e ?

Overturning Factor of Safety Check
Resisting Moment = 25k (2ft) = 50 k-ft
Destabilizing Moment = 5k (2ft) + 10k (2ft) = 30 k-ft
Overturning Moment FOS = 50 k-ft/ 30 k-ft = 1.67
Now, if you consider the resultant load eccentricity and the relationship, Overturn Factor of Safety = L/2e (where L if the footing length, 4ft):
e' = 4ft - (50k-ft - 30k-ft)/25k = 3.2 ft
Eccentricity, e = 3.2ft - 4ft/2 = 1.2 ft
Overturn FOS = L/2e = 4ft/(2 x 1.2ft) = 1.67, OK
When I calculate the bearing stress, my approach is, qmax = (2 x 25k) / [(3 x 4ft)(4ft/2 - 1.2ft)] = 5.20 KSF
However, if you enter the same criteria in Enercalc, you get approx. 1.875 KSF, achieved by:
e' = 4ft - (50k-ft - 30k-ft)/(25k - 10k) = 2.67 ft
Eccentricity, e = 2.67ft - 4ft/2 = 0.667 ft
Overturn FOS = L/2e = 4ft/(2 x 0.667ft) = 3.0, DOES NOT EQUAL 1.67
qmax = [2 x (25k-10k)] / [(3 x 4ft)(4ft/2 - 0.667ft)] = 1.875 KSF
My question is, what is the best way to handle the destabilizing uplift load? And why does Enercalc's method not maintain the relationship where OT FOS = L/2e ?
