Logan82
Structural
- May 5, 2021
- 212
Hi,
I want to follow up on this post ( but with a slightly different question.
The assumptions are the following:
- Inertiatotal = Inertiabottom_beam + Inertiatop_beam (this was the conclusion of this thread (- The top beam has less inertia than the bottom beam
- The two beam shapes are different.
- The two beams are not linked to each other, they are just stacked.
- We can assume that there is no friction.
- The two loads are symmetrical.
- In reality there are bolts, but there are not enough bolts to make sure that the two beams are linked.
- The deflections of the two beams are equal (δ1 = δ2).
I have the following situation:
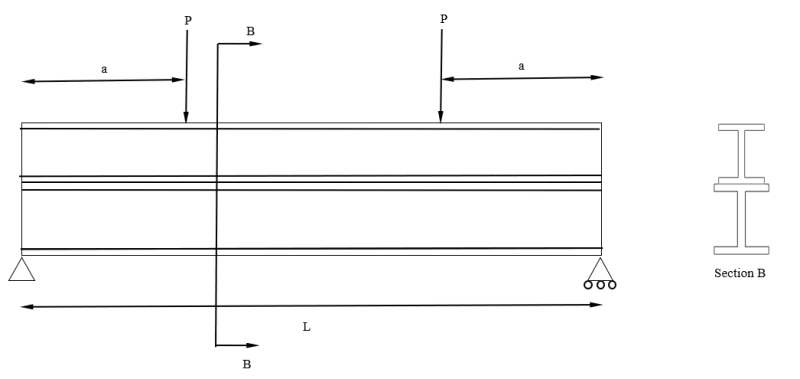
Questions:
- What would be the maximum strain at the tension fibre of one of those two stacked beams?
- More specifically, what should I take for the distance between the neutral axis and the fiber in tension "y"?
I want to follow up on this post ( but with a slightly different question.
The assumptions are the following:
- Inertiatotal = Inertiabottom_beam + Inertiatop_beam (this was the conclusion of this thread (- The top beam has less inertia than the bottom beam
- The two beam shapes are different.
- The two beams are not linked to each other, they are just stacked.
- We can assume that there is no friction.
- The two loads are symmetrical.
- In reality there are bolts, but there are not enough bolts to make sure that the two beams are linked.
- The deflections of the two beams are equal (δ1 = δ2).
I have the following situation:

Questions:
- What would be the maximum strain at the tension fibre of one of those two stacked beams?
- More specifically, what should I take for the distance between the neutral axis and the fiber in tension "y"?
