Strain in compression rebar of doubly reinforced beams.

[M_U]

Hi,
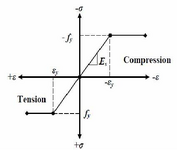
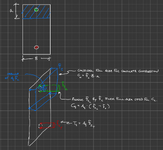
I am little confused with values of the strains in the compression rebars in doubly reinforced beam. Is there any limit on the strain of the rebars. Should the stress be within yield stress or it may exceed yield stress values. If the stress in rebars exceed the yield strength, then the strain may be higher than 0.003 limit for top compression fiber of concrete. please guide me on this.

Thanks.

 

[EngDM]

Typically you set your stresses in the bars to the yield stress, run through your stress block equations (meaning Fy = 400MPa or whatever bar stress your code uses), and then use strain compatibility with the max concrete compressive strain to determine your steel strain. If your steel strain then exceeds the yield strain, you have confirmed your initial assumption that steel yields. If steel doesn't yield, you either go back and adjust the number of bars to ensure it does yield, or run through your stress block calcs and the strain calcs with the new fs, and iterate until your fs stress converges.

 

[M_U]

Typically you set your stresses in the bars to the yield stress, run through your stress block equations (meaning Fy = 400MPa or whatever bar stress your code uses), and then use strain compatibility with the max concrete compressive strain to determine your steel strain. If your steel strain then exceeds the yield strain, you have confirmed your initial assumption that steel yields. If steel doesn't yield, you either go back and adjust the number of bars to ensure it does yield, or run through your stress block calcs and the strain calcs with the new fs, and iterate until your fs stress converges.

Thanks for the reply. But my concern is that if the yield stress in the compression rebar exceed yield strength. Then if I refer ACI value, the min yield strain for grade 60 rebar is 0.002. And if the forces in the compression rebars are higher then the strain in these rebars may exceed 0.003 which is the limit for top compressive fibre for concrete. Then there may be a problem? Please correct me if I am wrong.

 

[EngDM]

Thanks for the reply. But my concern is that if the yield stress in the compression rebar exceed yield strength. Then if I refer ACI value, the min yield strain for grade 60 rebar is 0.002. And if the forces in the compression rebars are higher then the strain in these rebars may exceed 0.003 which is the limit for top compressive fibre for concrete. Then there may be a problem? Please correct me if I am wrong.

You set the value for fs = fy (steel stress = steel yield) then calculate your stress block depth. Then using strain compatibility you verify your assumption that fs is indeed fy, or 0.002 as you've mentioned. If your value of es exceeds esy of 0.002, then great, your assumption is correct. And since you used fs = fy when calculating stress block, the moment resistance you calculate will be correct and conservative. I think what is confusing you is that yes, you can calculate a strain larger than 0.002, but you don't actually use that value when calculating Mr, I.E. it's not like you back calculate an fs of greater than what the yield is and then use that value in the T = C calculations; the strain check is only to verify your assumption that the fs = fy.

The only time you use anything other than Fy for the Tr = phi*As*Fy portion of the equation is when you calculate your steel strain and it is less than 0.002; in this case you have to iterate until you converge on a solution of what fs is actually equal to. This is more likely to happen in an over-reinforced section.