NAFTALI-HAKOHEN
Civil/Environmental
hi,
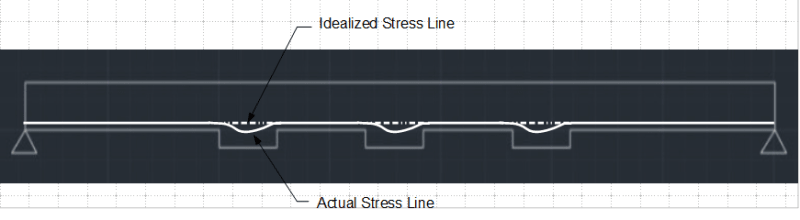
had an argument with my boss today about stress distribution in a beam with small 'teeth' sticking out in tension area, bottom of beam:

i said there will not be tension stress in the teeth , obviously depending on the dimensions an ratio of width/depth etc, somehow as a gut feeling that is has to do with the flow of shear tau into this small area ,
i then did a FEM model to confirm this and i think this is correct,
can someone explain the theory behind this or post some links?
thanks
Naftali
had an argument with my boss today about stress distribution in a beam with small 'teeth' sticking out in tension area, bottom of beam:

i said there will not be tension stress in the teeth , obviously depending on the dimensions an ratio of width/depth etc, somehow as a gut feeling that is has to do with the flow of shear tau into this small area ,
i then did a FEM model to confirm this and i think this is correct,
can someone explain the theory behind this or post some links?
thanks
Naftali

![[pipe] [pipe] [pipe]](/data/assets/smilies/pipe.gif)