feelthismoment18
Student
- Feb 16, 2025
- 7
Hey there,
I'm doing my masters research problem on the folding of origami inspired triangulated cylinders and I am currently trying to build some code that simulates this folding process.
The simulation so far is a bunch of pin-joint bars that make up the 'folds' and will deform under an axial load (as shown below). I have managed to create a massive global stiffness matrix for these bars.
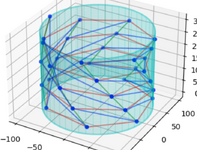
My problem is that in order to distribute the axial load to the nodes properly, I need to use a rigid plate. The paper I have attached goes into detail about various equations for compatability and equilibrium of forces and moments in the plate but my problem is that I am not sure how to apply these to be able impliment the plate into the stiffness matrix and be able to solve for forces and displacements in the structure as a whole.
If there is anyone that is able to look over what I've sent and help me or point me in the direction of somewhere else to look for answers it would be very helpful.
Thanks <3
I'm doing my masters research problem on the folding of origami inspired triangulated cylinders and I am currently trying to build some code that simulates this folding process.
The simulation so far is a bunch of pin-joint bars that make up the 'folds' and will deform under an axial load (as shown below). I have managed to create a massive global stiffness matrix for these bars.

My problem is that in order to distribute the axial load to the nodes properly, I need to use a rigid plate. The paper I have attached goes into detail about various equations for compatability and equilibrium of forces and moments in the plate but my problem is that I am not sure how to apply these to be able impliment the plate into the stiffness matrix and be able to solve for forces and displacements in the structure as a whole.
If there is anyone that is able to look over what I've sent and help me or point me in the direction of somewhere else to look for answers it would be very helpful.
Thanks <3

