Structure Stability 2

[Hudhaifa]

Hi

The stability concept of a structure (frame/truss) is not very clear for me. I have found the following statement in one of the structural courses;

What do you think about the above statement?

 

[rowingengineer]

I really like them, looks like a good course, makes you think about stress vs strain relationships.

http://www.nceng.com.au/

"Programming today is a race between software engineers striving to build bigger and better idiot-proof programs, and the Universe trying to produce bigger and better idiots. So far, the Universe is winning."

 

[robyengIT]

the two statements are saying the same thing : in positive form and negative form (two negations = affirmation)

 

[hardbutmild]

the two statements are saying the same thing : in positive form and negative form (two negations = affirmation)

I'm not sure that they are. The first one is not saying anything about when the structure is stable.
So based only on the first statement if the displaced shape can be drawn so that members deform, maybe there's something else that you need to check to ensure the stability. The second statement basically means that there's nothing else.

That's what's bothering me here, the second statement which implies that if any member in a structure deforms under a load, the structure is stable.
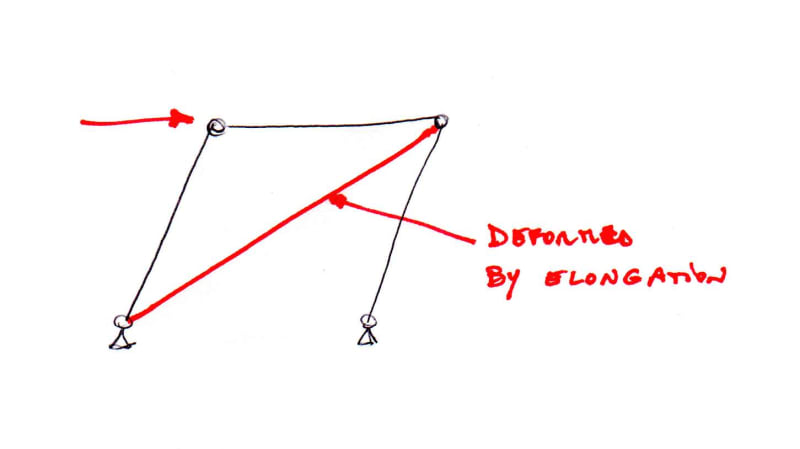
Isn't the instability possible even if some of the elements deform, like the picture below?

You can not draw a displaced shape without causing a deformation of an element, right?
What am I missing here?

 

[robyengIT]

possible instability, wrong design sure

 

[hardbutmild]

Of course it's wrong design, that was my point... the fact that an element deforms does not necessarily mean that the structure is stable.

 

[phamENG]

My impression is this:

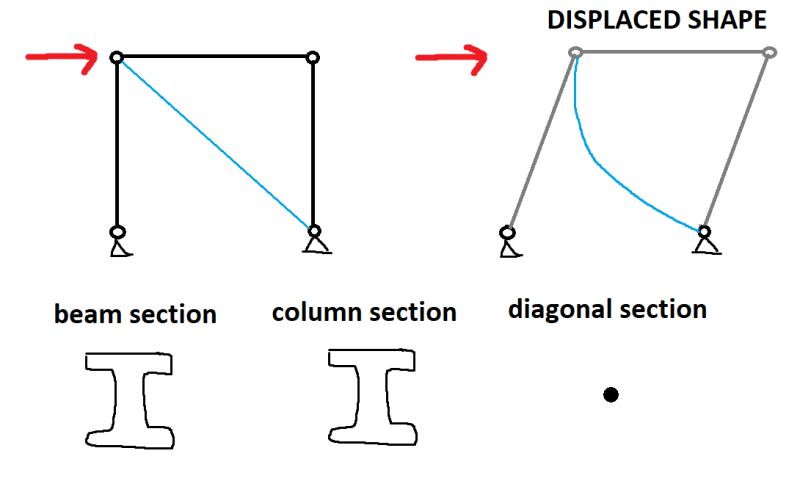
If no members deform, then all of the joints are released and no member resists the lateral force - it just racks over without the members noticing anything is happening.

If a member has to deform, then there is some resistance somewhere to the lateral force - it could be a moment connection inducing flexure and flexural deformation or it could be a diagonal brace with axial deformations.

These are clearly VERY general. Any structure can be made unstable by applying a large enough load.

 

[r13]

What am I missing here?

You didn't miss anything. The author of those statement missed to address that rod/cable/light gage bracing is an exception due to the lack of axial compressive strength. Otherwise, the statements make good sense.

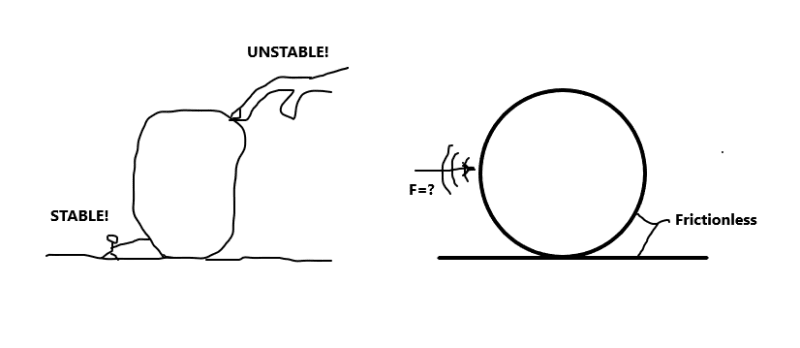
IMO, instability is a phenomenon that a object, when subjects to external force, can change its position freely. The magnitude of the force plays a role only when the frictional force is involved.

 

[phamENG]

r13 - I generally agree with your view that when subjected to an external force, an unstable frame will move freely. I do not, however, agree that the magnitude of the force only plays a role when dealing with friction.

If you apply a sufficient force to a moment frame, the rigid joints will yield and form plastic hinges, making it unstable so long as the plastic moment capacity is exceeded or completely unstable if pushed to the point of material rupture.

If you apply a sufficient force to a braced frame, the brace will buckle and force the frame to go from stable to unstable - either temporarily with elastic buckling while the load exceeds the elastic buckling capacity of the member, or permanently if the brace buckles inelastically. If a tension brace, then you have a similar issue from above with yielding of components (or failure of the connections).

 

[r13]

pham,

You are thinking the stability in the limit state, a phenomenon/cycle started with a "stable" structure that is forced to move, and the member were stressed/deformed. Prior to the members/joints fail in strength it is in limit stability (ultimate), then after the mechanism forms, the structure is said to be unstable, because theoretically, no additional force is required to cause it to collapse (a free, unrestricted movement). On the other hand, an unstable structure will not go through this cycle to change its position though.

Your claim fits the situation if both gravitational force and friction are brought into the picture. Think about the ancient stone structures that still stand, and for example, a 10 tons rock on the ground, obviously it needs a huge force to push it over. However, before it moves, can we say it is unstable?

 

[phamENG]

it needs a huge force to push it over. However, before it moves, can we say it is unstable?

Yes.

 

[r13]

 

[Tomfh]

Isn't the instability possible even if some of the elements deform, like the picture below?

The 2nd picture is stable, however it has such extremely low capacity (due to rod buckling quickly) that we say imagine it to be unstable.

 

[phamENG]

r13 - Nice.

 

[r13]

pham, thanks.

 

[Blackstar123]

All good explanation above. Just wanted to give my own version of a simpler explanation.

1. An external force that does not produce any internal deformation in a body is said to be in rigid body motion and thus, is considered unstable from structural point of view.
2. Similarly, when a force produces internal deformation in a body (that is, its ability to resist that force), is structurally considered to be stable.

I've underlined the key words in your snippet that should be the main focus of the statement.

 

[Hudhaifa]

1. An external force that does not produce any internal deformation in a body is said to be in rigid body motion and thus, is considered unstable from structural point of view.
2. Similarly, when a force produces internal deformation in a body (that is, its ability to resist that force), is structurally considered to be stable.

This is exactly what I understood from the statements.
The internal deformation of a member or members in a structure exhibits a resistance against collapse and thus the structure is stable in which can stand the applied load (within the ultimate load).

The course itself shown the following examples for more clarification,

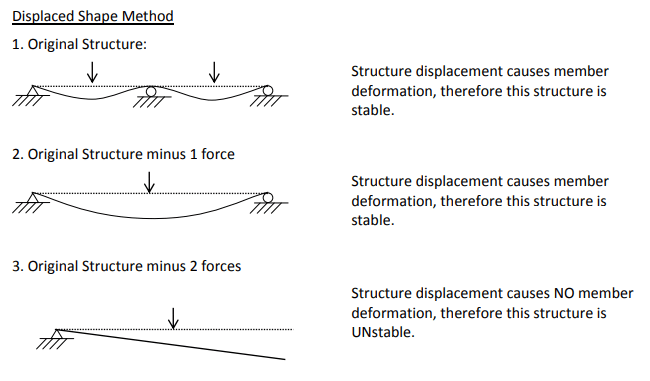
The only mistake in the example below at the structure No. 3, the right side support is supposed to be pin not fixed. So considering pin support reflects the earlier mentioned statements about stability.

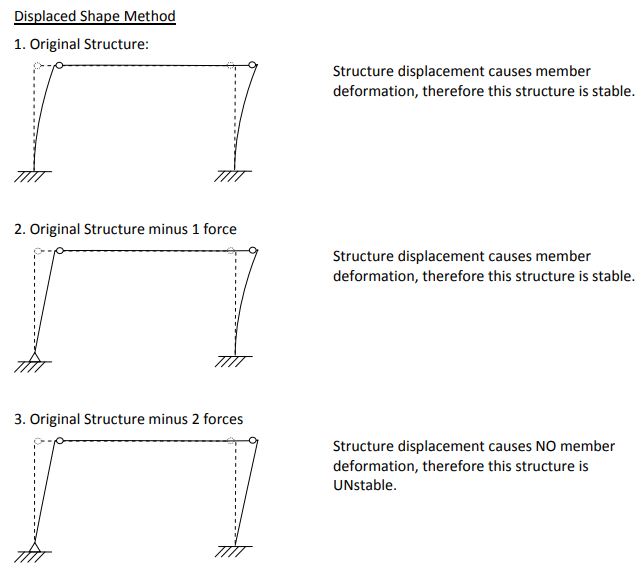
I do agree with all above explanations that any structure becomes unstable by applying large enough load greater than its ultimate strength.
But the idea here about the stability with respect to linear-elastic behaviour and small-displacement theory.
In other words, we want to check does the structure collapse under the applied load or an internal deformation of a member/members show resistance to such extent.

 

[rb1957]

don't confuse structural failure, like column buckling, with "structural instability".

an "unstable structure" is a mechanism. It doesn't have enough loadpaths to react the applied load.

As for your frame pictures, it's not clear to me when a joint is fixed or when it is pinned; maybe fill in the circles for a fixed joint ?
the 1st frame would appear to have two fixed joints (to the vertical members),
the 2nd 1 and the 3rd none (and so it'd fall over under load).

another day in paradise, or is paradise one day closer ?

 

[r13]

rb,

Circle usually indicates a hinge joint, either with both ends of the connected members released of without rotational restrain, or only one member end released of rotational restrain. In the above frames, both ends of the roof member are released, while the upper joint of the columns has all three restrains (no release).

 

[rb1957]

I see just about no difference in the 3 models. Obviously the displaced shapes are drawn from the understanding of the joint condition.

another day in paradise, or is paradise one day closer ?