Hi guys,
I'm dealing with a situation where a thin plate is subjected to an in-plane stress and expected to buckle, which is no concern for the strength of the structure - but I am interested to know how to calculate the theoretical out-of-plane deflection of the plate so I can check if this will cause any unforeseen problems.
The critical stress is calculated from the below equation with kc = 4.0 (both longitudinal edges are pinned):
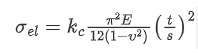
With t = 6 mm, v = 0.25, E = 200,000 MPa and s = 1930 mm ---> critical stress is 6.8 MPa. This is confirmed by a quick FE model:

The out-of-plane deflection shown above (generated by the linear buckling model) does not have any physical significance, as far as I know - only useful in terms of relative deflection (or 'shape').
Instead, I performed a nonlinear analysis on the plate and monitored the out-of-plane deflection vs applied stress. As you can see below, the plate remains perfectly flat until the buckling load is reached (at about 7 MPa), and then suddenly forms the buckled shape.
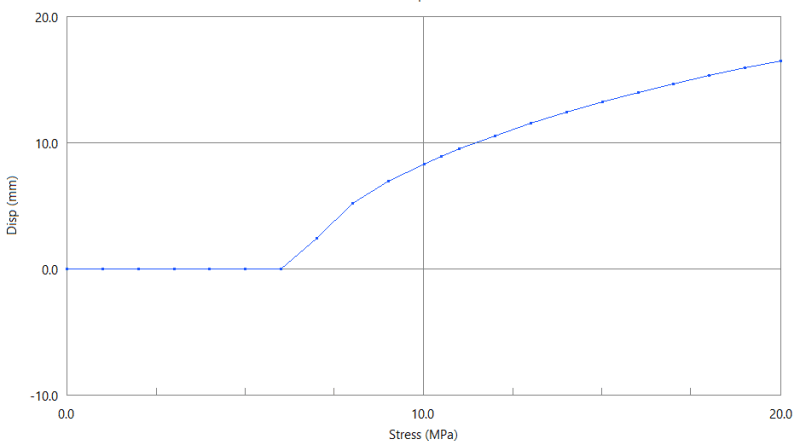
Is there any way that the out-of-plane deflection can be calculated for a given stress (greater than the critical buckling stress)? I would like to verify the FE results with something theoretical ideally.
Thanks!
I'm dealing with a situation where a thin plate is subjected to an in-plane stress and expected to buckle, which is no concern for the strength of the structure - but I am interested to know how to calculate the theoretical out-of-plane deflection of the plate so I can check if this will cause any unforeseen problems.
The critical stress is calculated from the below equation with kc = 4.0 (both longitudinal edges are pinned):
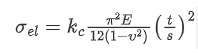
With t = 6 mm, v = 0.25, E = 200,000 MPa and s = 1930 mm ---> critical stress is 6.8 MPa. This is confirmed by a quick FE model:

The out-of-plane deflection shown above (generated by the linear buckling model) does not have any physical significance, as far as I know - only useful in terms of relative deflection (or 'shape').
Instead, I performed a nonlinear analysis on the plate and monitored the out-of-plane deflection vs applied stress. As you can see below, the plate remains perfectly flat until the buckling load is reached (at about 7 MPa), and then suddenly forms the buckled shape.

Is there any way that the out-of-plane deflection can be calculated for a given stress (greater than the critical buckling stress)? I would like to verify the FE results with something theoretical ideally.
Thanks!

![[smile] [smile] [smile]](/data/assets/smilies/smile.gif) .
.