l______40mm______l
Structural
- Jul 19, 2020
- 16
Hi,
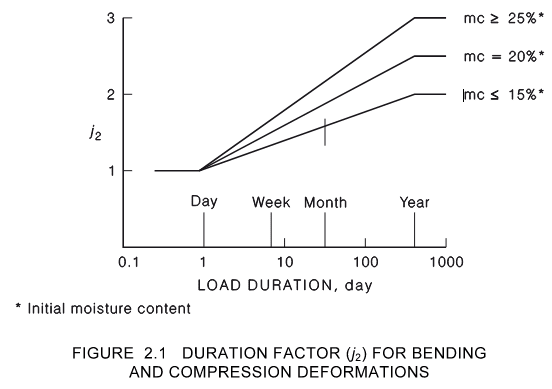
I'm an Australian structural engineer and am currently trying to define the total deflection criteria for a timber floor. In the Australian standard AS1720.1 you determine a modification factor for creep (j2). The dead load deflection is noted by δG and the live load deflection is noted by δQ.
TEDDS design software uses a total deflection criteria of j2 x (δG + ψsδQ), ψs being the short-term component of the live load (0.7 for typical floor applications).
Structural toolkit design software uses a total deflection criteria of j2 x (δG + ψlδQ)+ ψsδQ, ψl being the long-term component of the live load (0.4 for typical floor applications).
Both formulas seem to be over-conservative to me as I thought that the criteria would be j2 x (δG + ψlδQ)+ (ψs-ψl)δQ, as you've already accounted for part of the live load in the creep formula.
I'm not an expert in Timber so any advice or comments would be greatly appreciated.
Cheers.
I'm an Australian structural engineer and am currently trying to define the total deflection criteria for a timber floor. In the Australian standard AS1720.1 you determine a modification factor for creep (j2). The dead load deflection is noted by δG and the live load deflection is noted by δQ.
TEDDS design software uses a total deflection criteria of j2 x (δG + ψsδQ), ψs being the short-term component of the live load (0.7 for typical floor applications).
Structural toolkit design software uses a total deflection criteria of j2 x (δG + ψlδQ)+ ψsδQ, ψl being the long-term component of the live load (0.4 for typical floor applications).
Both formulas seem to be over-conservative to me as I thought that the criteria would be j2 x (δG + ψlδQ)+ (ψs-ψl)δQ, as you've already accounted for part of the live load in the creep formula.
I'm not an expert in Timber so any advice or comments would be greatly appreciated.
Cheers.