time series analysis - finding the linear trend in a random walk

[GregLocock]

This is a bit of a roundabout question.

So, if you have a short series of samples, say 135, could you determine whether there is a linear signal buried in the noise? Imagine that the series is a random walk ie value= value(n-1)+ a signed random variable + X. The signed random variable is of the order of +/- 0.5 say +/- 3 sigma limits. X might be .01

Apparently the answer is no, but I wondered if a technique that measured how many attempts /on average/ it took to find a random number sequence that sufficiently matched the 135 long record for a given assumed value of X was (a) known or (b) a plausible way of investigating the best value of X? Or even graph the average number of tries to meet an RMS error value vs X?

You may know the background to this question or you may not. I'll reveal all later

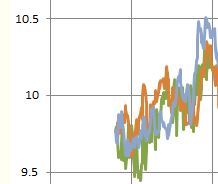
Here's a plot, the green curve is real world data, the other two are random walks. One of the random walks is just random, the other has a gradient superimposed on it. I am looking for a way of reliably assessing whether there is a linear trend underneath the random walk.

Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376

http://eng-tips.com/market.cfm?

 

[IRstuff]

I don't think there's definitive way to distinguish them; it's the nature of the random walk that you can get anything possible, although the tendency is to move away from the starting point. We basically talk about "drift" for devices with random walk, as if there was a linear behavior. But, "drift" is essentially a mean value of random behavior.

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert!

https://www.youtube.com/watch?v=BKorP55Aqvg

faq731-376 forum1529 Entire Forum list

http://www.eng-tips.com/forumlist.cfm

 

[GregLocock]

So I've set up a spreadsheet with two different values of X

Then test how long it takes for each series to converge to a given goodness of fit to the original data. repeat several times, this gives a score for each X.

Is speed of convergence to a good fit a statistical technique with a proper name ? It sounds like something a machine learning or optimiser would use, and we use it as an indicator of the quality of our MBD models - good clean models run fast, horrible buggy cludged models like mine take forever.

Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376

http://eng-tips.com/market.cfm?

 

[IRstuff]

I think that for such a short sequence, it will always be possible to find a trend line; whether it maintains itself over time is a different matter. This is pretty much the situation with the global warming argument about the last 30 years.

It seems to me that it would be easier to do this the other way around, i.e., take your trend and determine its fit to a straight line and decide whether the calculated sigma is plausible or consistent with your process. The bottom line is that if you see something that looks like it has a linear trend, you can find a line that "fits," only it might be rather a cruddy fit; the measure of fit would still default to the regression coefficient and the calculated deviation from a perfect line.

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert!

https://www.youtube.com/watch?v=BKorP55Aqvg

faq731-376 forum1529 Entire Forum list

http://www.eng-tips.com/forumlist.cfm

 

[GregLocock]

That assumes a model. Admittedly assuming a random walk plus 'drift' is also a model, the question I am looking at is if there is an untraditional way of identifying a small linear signal in a short noisy time series. Specifically, in value= value(n-1)+ a signed random variable + X if we run the random walk for Z cycles, and plot Z as a function of least rms error, does that provide some insight into X?

Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376

http://eng-tips.com/market.cfm?

 

[IRstuff]

I don't think so; generally, a random walk shows rather huge variances, relative to the straight line, as indicated in your data.

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert!

https://www.youtube.com/watch?v=BKorP55Aqvg

faq731-376 forum1529 Entire Forum list

http://www.eng-tips.com/forumlist.cfm

 

[GregLocock]

Thanks for paying attention to this, it turns out, as you sort of imply, that it doesn't really work, at least for the case I was interested in.

Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376

http://eng-tips.com/market.cfm?

 

[IRstuff]

No worries; sorry it didn't work out.

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert!

https://www.youtube.com/watch?v=BKorP55Aqvg

faq731-376 forum1529 Entire Forum list

http://www.eng-tips.com/forumlist.cfm