I am carrying out a feasibility study on whether a site has potential for the installation of an energy production system.
The site is tidal and fills a pond through a sluice once the tide has come in, similar to the picture below.
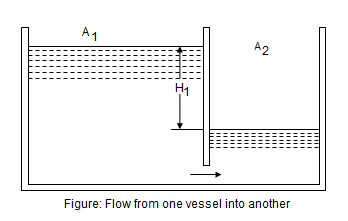
I need to find the time taken for the pond to fully fill so the head difference is 0. I have been using the below equation, but it takes into account the area of the large container when in reality this is the sea so it is infinite. I could just make A1 extremely large but i'm not sure how accurate this is.
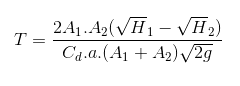
Where:
T = Time to fill (s)
A1 = Area of large container (this is actually the sea)
A2 = Area of pond
H1 = initial head difference
H2 = Final head difference (=0)
Cd = Discharge coefficient
a = area of orifice
The site is tidal and fills a pond through a sluice once the tide has come in, similar to the picture below.

I need to find the time taken for the pond to fully fill so the head difference is 0. I have been using the below equation, but it takes into account the area of the large container when in reality this is the sea so it is infinite. I could just make A1 extremely large but i'm not sure how accurate this is.
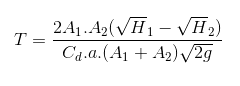
Where:
T = Time to fill (s)
A1 = Area of large container (this is actually the sea)
A2 = Area of pond
H1 = initial head difference
H2 = Final head difference (=0)
Cd = Discharge coefficient
a = area of orifice
