Transformer S11 parameter analysis 1

[zappedagain]

I’m a bit rusty on my S-parameters and I ran into something interesting (about 9 questions worth). I’m attempting to determine the leakage inductance on a transformer. Measuring the inductance at the switching frequency is straightforward, but the only equipment I can measure with at the ringing frequency is a VNA. I get some interesting plots on the Smith Chart so I’m looking for confirmation of my findings.

Does the long wire length in the transformer introduce a time delay (transmission line effect)? I ask because the impedance keeps looping (clockwise) around the Smith Chart as the frequency increases. Is there a way to model this or calibrate it out? Or is there another explanation?

Here is the plot of S11 on the primary with the secondary open circuit:

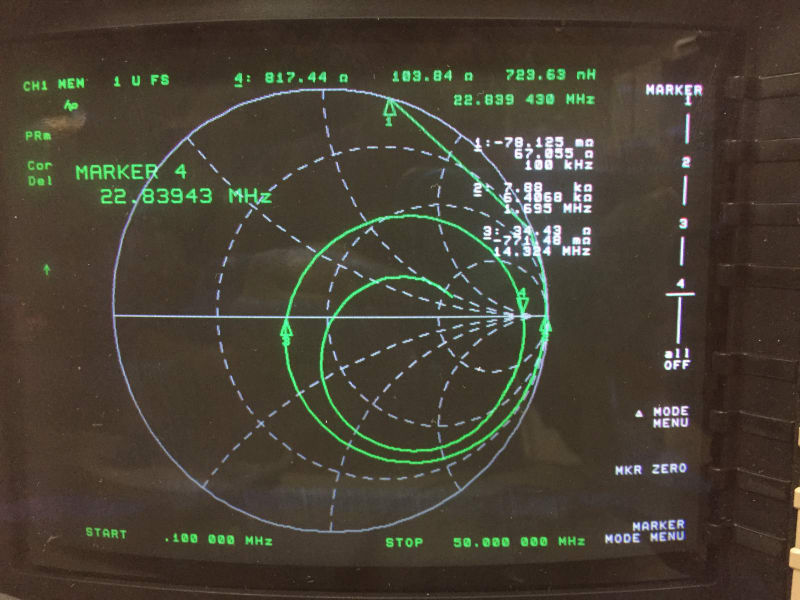
Marker 1 is at 100 KHz and shows my expected inductance of 106 uH (67 jOhm). That make sense.

At frequencies above that the inductance increases, with Marker 2 showing 6.4K at 1.7 MHz (106 uH is 1.1K jOhm). I’m assuming this is a change in the magnetic core properties with frequency.

Marker 2 at 1.7 MHz appears to be the self-resonant frequency (SRF), as I cross from positive (inductive) to negative (capacitive) at higher frequencies.

Marker 3 at 14 .3 MHz seems to indicate a null in the impedance (34 ohm); is this where the parasitic inductance on the parasitic capacitance starts to come into play?

Marker 4 indicates another SRF harmonic at 22.8 MHz. This isn’t at an integral multiple of Marker 1 (1.7 MHz), so is that an improper interpretation?

It seems like the long wire length in the transformer is introducing a time delay (transmission line effect) as I keep looping (clockwise) around the Smith Chart as frequency increases. Is there a way to model this?

My turns ratio is 3:1. Could I put a 5.5-ohm resistor across the secondary (looks like 50 ohm on the primary) and tune out this shift with an electrical delay parameter?

Here is what S11 looks like with the secondary shorted:

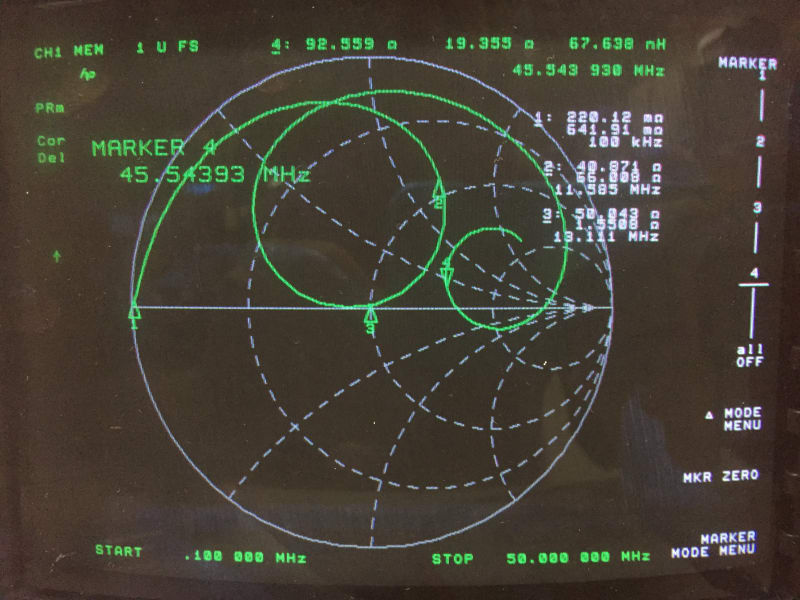
Why did the center of the rotation shift upward into the inductive region?

Marker 1 = 0.64 jOhm at 100 KHz (! 1 uH, that’s reasonable)

Marker 2 = 40 + j66 Ohm at 11.6 MHz, a null in the S11 magnitude display (half of the frequency of the Marker 4 in the open secondary plot; coincidence?)

Marker 3 = 18 nH at 13.1 MHz shows an almost a perfect 50 ohm impedance; I can’t explain that one.

Maker 4 = 67 nH at 45.5 MHz. Can this be explained by core non-linearities?

Thanks for reading this far!

Z

 

[zappedagain]

Aww, nobody wants to tackle this one?! Z

 

[VEBill]

I've never had the need to go that deep into a transformer.
Of course I've heard about Leakage Inductance, but I've not had to apply it (in memory).

With a Google search _(sorry...) on: Measuring Leakage Inductance
a nice tech note showed up at Rackcdn.com
Ref: Measuring Leakage Inductance - VOLTECHNOTES (VPN 104-105/3)
(Google seem intent on making it impossible to capture direct links to the PDF. 3rd hit down, YMMV.)

It seems to be straightforward:
"Since LL (Leakage Inductance) is a function within the transformer, it is clearly not possible to measure its value directly. A method must therefore be used to subtract the value of LP from the total measured inductance. This is achieved by applying a short circuit across the secondary terminals (figure 5). A perfect short circuit will result in zero volts on the output terminals (figure 6) and, through transformer action, zero volts will also appear across the primary inductance. The measured value of inductance at the primary terminals will therefore be the true leakage inductance (LL)."

Short the output, measure the Leakage Inductance directly.

As always, keep your wits about you and triple-check everything six ways from Sunday.

 

[zappedagain]

I'm not so much interested in how to measure the leakage current; On Semiconductor has a very good procedure defined on p. 4 of their AN1679-D Application Note. I'm more interested in the S-parameter analysis on the Smith Chart. Such as:

Why is my measurement moving clockwise (toward the generator) as frequency increases? That seems like the opposite effect of a time delay.
Is this real or a calibration issue?

What defines the center of the circle of rotation as the measurement moves?

Why do what appear to be resonances not occur at integral harmonics?

Thanks,

Z

 

[VEBill]

"I’m attempting to determine the leakage inductance on a transformer."

!!!!

As far as I've seen, Smith Charts go clockwise with increasing frequency (I believe simply because of the way they're laid out), and generally spiral into the center due to increasing loss with frequency. The attractive center represents the selected Zo of the chart (e.g. 50 ohms 'dummy load' equivalent), and loss generally goes up with frequency. So they'll all eventually end up in the middle, if you go high enough.

Your "center of rotation" seems to be a visual artifact of your smooth measurements. The one time (!) that I used a Smith Chart in anger, the line was squiggly and had little loops within the larger loop. It didn't really indicate a center of rotation, but was generally orbiting around its next destination on the long road to the lossy 50-ohm center of the chart. In my example, the curve approximately circled around the design impedance approximately centered within the design frequency range. They couldn't hit the design impedance exactly, but they did a good job in centering it up as best they could. Close enough for antenna matching.

The 'resonances' would be influenced by the increasing impact of other subtle effects with increasing frequency. Those subtle effects would come into play with increasing frequency and result in non-integer relationships of what you're seeing. That not-precisely integer relationship thing is pretty common in all sorts of systems. In music, it's noted that overtones are sometimes not precisely integer multiples of the fundamental. Your example would be much worse, perhaps due to the core material.

It should be obvious that I'm not a top expert on this. But I hope that the above is reasonably correct and helpful. If your situation is critical, then check with others.

 

[zappedagain]

Did I say that?! Sorry for the misdirection The measuring leakage at higher frequencies is the not so normal part...

Google popped up 2002Thuringer.pdf and that paper confirms a lot of my assumptions. Inductance increases as you move clockwise (Z = sL so inductance increases with frequency too), and Capacitance decreases while you move clockwise (Z = 1/sC so capacitance decreases with frequency too). So all the clockwise rotation with frequency is normal.

The proper term for clockwise rotation is "wavelengths toward the generator"; that makes sense as higher frequencies have shorter wavelengths so the number of wavelengths down a transmission line increases with frequency.

Your comment about circling the nominal impedance (50 ohms) makes sense. I suspect circling another point indicates a circuit with a different characteristic impedance (defined by the turns ratio, maybe?). The circling happens past the first SRF, so this may get into a lumped element model (primary inductance in parallel with stray capacitance that has its own series inductance that has its own stray capacitance, and so on...). Microwaves101 hints that there may be a way to determine the characteristic impedance with three measurements (

https://www.microwaves101.com/encyclopedias/measuring-characteristic-impedance#smith).

My data is spiraling so it might be a bit trickier.

Z

 

[VEBill]

...determine the characteristic impedance with three measurements... My data is spiraling so it might be a bit trickier.

Assuming that you're still referring to your transformer, then be aware that transformers themselves are not usually described as having a 'characteristic impedance'.

A transformer may be designed to operate effectively at, for example, 50-ohms. But you'd be hard-pressed to find anything resembling a 50-ohm measurement in the transformer by itself.

Of course, if you loaded a 1:1 transformer output with a 50-ohm load, then the 50-ohm should be seen on the input side. Plus or minus the transformer being non-ideal.

Getting in the weeds, a "50-ohm" transformer in a box may be equipped with 50-ohm design impedance connectors and possibly internal 50-ohm cabling as well. With expert TDR measurements, one might just be able to detect the Zo of those wee little ancillaries.

 

[zappedagain]

My (self) explanation for this so far is that once I'm in the transformer I no longer have a 50-ohm characteristic impedance. As I continue traveling away from the generator I circle (swirl around) the new characteristic impedance.

In the end I found this analysis didn't point to the solution; stray capacitance was the culprit.

Z