Ultimate Shear Of RC Beam/Column excluding the contribution of shear reinforcement.

[NTCONLINE]

Hi everyone,

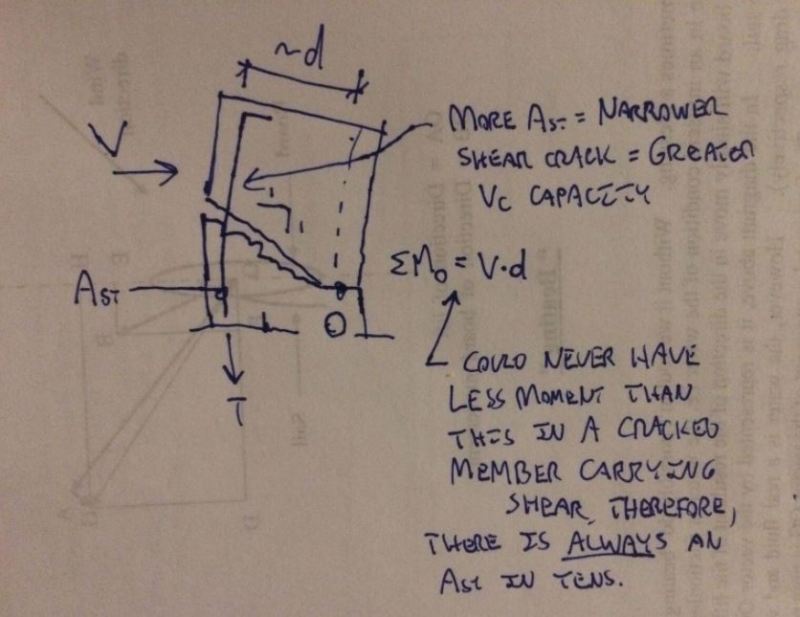
In most international codes, the shear of the concrete alone (excluding the contribution
from shear reinforcement) is in the form of, for example, in AS3600:

Vuc = Beta1 * Beta2 * Beta3 * bv * do * fcv * (Ast/(bv*do))^ 1/3

Each code has its own expression, but in general, Vuc is mathematically
in a form of a direct function of Ast, which is the steel in tension, under the
load case being considered.

If Ast = 0, (ie. there is no steel in tension at all, or all steel rebars are in compression)
Vuc will be equal to zero, mathematically.

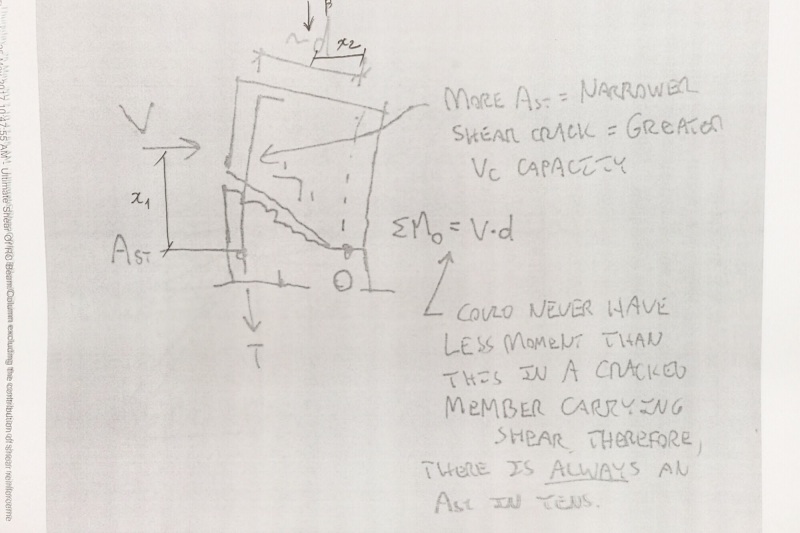
Let's consider a rare scenario, where there is a RC column under only axial force
acting right at the plastic centroid of the column section. Therefore, the axial force
does not cause any bending at all. In this case, based on the above equation,
Vuc = 0, which does not really make any sense to me, because in such a case, the column
shear capacity is even at its highest possible value.

How should I really interpret the parameter "Ast" in the above equation ?

 

[KootK]

I practice in north america where the shear provisions take a different form. So I may not be the best person to respond to your question. However, since nobody else seems to be chiming in, I'll give it a whirl. One of the primary mechanisms of shear transfer in cracked concrete is aggregate interlock and shear friction across the flexural compression block. And you can't really have a flexural compression block without some steel in tension to balance that out in ordinary flexural members. My suspicion is that your "steel in tension" is attempting to capture that phenomenon.

Let's consider a rare scenario, where there is a RC column under only axial force acting right at the plastic centroid of the column section. Therefore, the axial force does not cause any bending at all. In this case, based on the above equation, Vuc = 0, which does not really make any sense to me, because in such a case, the column shear capacity is even at its highest possible value

Technically, this is a moot point as your shear demand is also zero in this scenario. I take your point though. In north america, we have provisions that allow us to account for the beneficial effect that prestress has on shear capacity. One could argue that reliable column axial load is effectively prestress from the perspective of shear capacity.


I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[NTCONLINE]

Hi KootK

Thank you for your reply.

There is no doubt that the shear strength provided by concrete , Vc, is taken as
the shear causing inclined cracking. After cracking, Vc is attributed to aggregate
interlock, dowel action, and the shear transmitted across the concrete compression zone.

As regards to the axial effect, the AS3600 and ACI code have identical factor to account for that,
which is (1 + N/14Ag) for compression and (1-N/3.5Ag) for tension.

What hit me was that the Australian Standard as well as the Eurocode has a factor "Ast",
which is the area of steel in tension zone, in their equation for shear.
This triggered me to think twice what I should do in case there is no steel tension zone at all, (like the scenario I stated above, or a very short column under compression load)

The ACI code makes sense, mathematically, in all cases, where Vc = 0.17 SQRT(fc) bw d (normal weight concrete) - which does not contain the term "Ast" at all.

 

[KootK]

You're most welcome NTC. How about this:

1) In a member loaded in shear, there really is no such thing as zero moment. At minimum, you'll always have at least the moment equivalent to V x d (sketch below).

2) Because of #1, a shear cracked member must always have some amount of flexural tension reinforcing (Ast). Were this not so, equilibrium simply could not be satisfied (sketch below again).

3) More flexural tension reinforcing means smaller shear cracks.

4) Smaller shear cracks means higher Vc shear capacity.

Taken in aggregate, points one through four mean that there's always some Ast in a shear cracked member. That pretty much addresses your question does it not? Really, it's not possible to have cracked Vc without Ast. In that sense, kudos to the AS/Euro provisions for capturing that.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[Settingsun]

AS 3600 section 15 has some guidance for plain concrete members (and also limitations on application of the guidance). That might give you what you're after since it just appears to be a thought exercise where the limitations are not too critical.

 

[NTCONLINE]

hi KootK

Thank you for the sketch, it all makes sense perfectly.

I think the lever arm should be the distance x1
instead of "d" ?

I drew on top of your sketch. My question is:

Case 1)What if there is load P acting on top of this short column
which makes all steel to be in compression, and also this load P
acting at an eccentricity causes a moment at 0 which happens to
be exactly same as moment at O caused by V.
In other words, P * x2 = V * x1 thus the sum of all moment about point 0 is zero.
Is that in that case, there is no Ast (no steel in tension)?

Case 2) Let's assume this is a bucky concrete block and there is no steel at all in it.
The block is under compression force P. and a horizontal force V
And I would like to determine if this "prestressed" block in sufficient for that shear force V
without having to have some steel rebar and/or ties in it? This certainly can happen in reality
for example, with force V being very small.

One would think that we would have to compare this force V to the Vc of this concrete block,
but the equation for Vc , again, requires Ast, or else Vc =0. This leads to the designer having to
put some Ast in the concrete, even though it may not be necessary ?

 

[KootK]

Case 1. Realize that Ast doesn't actually have to be in tension to count. It merely has to be available for use in tension should the shear crack tend to open up.

Case 2. You're deacribing a plain concrete scenario. I would assume that your code has a different provision for the shear strength of unreinforced members (steve's post).

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[rapt]

ACI has a simplified and a detailed method for calculation of Vc. The detailed method has a reinforcement ratio which is related to As in the same way as do the other codes!

I would take Ast as the reinforcement near to the more tensile (or less compressive) face (and not include the side face bars, only the bars at the extreme face!

 

[NTCONLINE]

Thank you Steveh49, KootK and Rapt for your input.

You were correct there is a separate provision for plain concrete for case 2,
which I should have done a thorough search before asking question for that scenario.

KootK, I like the way you explain Ast as "available" steel for tension. That way is better / clearer explanation for parameter Ast.

Rapt, if the As is distributed like in the below figure, what bars would you count for "Ast" in this case?

Correct me if I am wrong, but theoretically, based on the AS3600, I would need to determine the neutral axis for each load case, and therefore,
Ast for each load case would be different, thus Vuc.

However, determining the neutral axis is not a straightforward process. Note that the figure is showing the ultimate limit state,
where the strain in concrete has reached its ultimate strain (0.003). But under an arbitrary service load case, the forces (M* V*) may not cause the
concrete to reach that state yet.

What would you use for As in this case, practically ? Or any advice for designers in this case, and in case of circular columns ?

 

[rapt]

I think the Canadian code actually defines it as the reinforcement in the tension half of the section (I would take this as the more tensile half), so in this case probably the bottom 7 bars. The next 2 bars above them would appear to be on the centreline so are doubtful!

Kootk could confirm this for us, being Canadian!

The next AS3600 shear rules will probably follow this logic as has the latest AS5100 for bridges.

 

[KootK]

The general method of the CSA code simply defines the tension rebar as conventional As. So nothing fancy from us. Interestingly, the method specifically targets the strain at mid-depth as being the output of the calculation. I feel that kind of corroborates my suspicion that it's about keeping the shear crack closed up tight.

Estimation of concrete shear capacity is a rough science, even for structural engineering. So I wouldn't loose too much sleep over the precise definition of Ast in complex situations. For the oval example, I'd approach it on a "take what you need" basis. I'd probably start with the bottom five bars and, if that worked out, I'd go no further. If it didn't work out, I'd add some more bars. Note that as you add bars, "d" will shrink. So it may wind up being something of a moot point anyhow.

I find it curious that in the AS provisions, the Ast term lives under the cube root. Almost as though the rebar were a straight up improvement to the uncracked concrete strength.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[rapt]

Kootd

d would shrink, but Canadian code limits it to a minimum of .8D, so it would only shrink to a point!

the AS treatment of Ast using the cube root is from the old BS8110 rules!

 

[NTCONLINE]

The Eurocode 2 provision has similar form which has a form of Ast to the power 1/3.

I have found a commentary to the EC2, which, interestingly, discusses the same topic.
It states that the formula has 2 main advantages. The first being that it does not distinguish what type of
loading combinations being applied thus difficult to determine the according safety factor. The second is that the shear capacity goes to 0 when Ast = 0.

The wish for a simple , conservative value for Vuc leads to the formula: Vuc = C * flexural strength of concrete * bw * d, and the coefficient C varies between 0.3 and 0.75.
For the most conservative case, C = 0.3, and says, flexural strength = 0.6 *SQTR(fc)
Vuc = 0.17 SQRT(fc) which is exactly the same as provided in the simplified method of ACI code.

 

[rapt]

Personally I have no objection to flexural shear capacity Vc being 0 when Ast = 0. The whole logic of the truss analogy for shear is that there is a tension tie and as concrete is assumed to have no tensile strength, it must be provided by reinforcement. So Ast cannot be 0.