Understanding when a ductile part breaks

[Rocket_Science]

Hi, I am a mechanical engineering student and I wanted to ask some questions about design of mechanical parts so that they don't break, because I tried putting together all I learned so far and I noticed I have some gaps that apparently they didn't cover in my uni courses.

I think I already have a good grasp on how to design parts (made out of a ductile material such as steel) so that they do not yield due to a static load. The process is theoretically simple, you just have to make sure that for each point of the part you are considering, the Von Mises stress doesn't get bigger than the material yield strength. The part could be complex and the stresses inside could be difficult to determine, but in the end it all reduces to checking the VM equivalent stress.

My doubts are specifically about the breaking condition of a part, because so far they only taught me to design parts so that they don't yield. At university we only saw simple cases of breaking due to uniaxial tension and the net stress simply had to be less than the UTS of the material. In practice it is not always possible to prevent local yielding (as in small fillets, or where there are contact stresses) so usually you calculate the average stress and compare that to the UTS of the part in simple cases.

My understanding so far is that when a part is designed against breaking, you can no longer use a local failure criterion like Von Mises because stress redistribution happens and elastic stresses become kind of meaningless (or are there local failure criterions that work for this purpose?) so it is easier to use a non local criterion such as choosing a surface where you think the part will break and calculating the mean stresses there.

I chose some examples relative to bolted joints to better expose my doubts, not because my doubts are relative to bolted joints specifically, but because it is where I most often saw these kinds of problems appear.

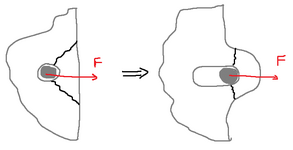
1) If we consider a bolt placed near an edge, to prevent tear out we check the mean stresses on the surfaces on the drawing:



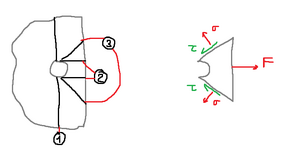
For surface 1 and 2 it is easy to determine if the part will break because the stresses will be only tension (1) or only shear (2). When it comes to surface 3 however it becomes more difficult to understand if the part will break, because after I find the shear and normal stresses on the surface, how do I understand if their current combination will result in breaking of the part? Again, I never heard of breaking criteria for ductile materials, only yield criteria, so I have no idea if the part will break along that surface or not.

2) Taking the same example as above, if I think about it even more, I then notice that I am also forgetting that the small material elements near the surface are also loaded by stresses in their surface perpendicular to the selected surface:



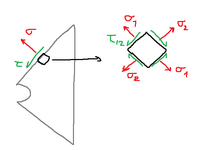
How do these stresses affect the breaking of the part? Do they even affect it? I ask because I don't remember ever considering them when doing these kinds of verifications, but in principle one should not forget them.

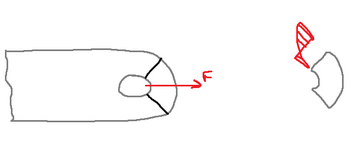
3) When I have the scenario shown in the drawing below, how can I determine how much of the force will be acting as shear and how much will be acting as normal stress?



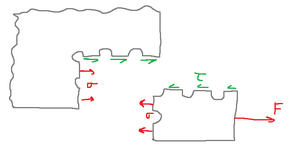
To verify that this kind of failure doesn't happen, I can just make sure that neither of the mean stresses on the two surfaces is bigger than the ultimate tensile/shear stress of the material. The difficulty is understanding how the load divides itself here. To add to this I also don't remember having ever seen the ultimate shear stress of a metal being tabulated somewhere, and I am quite sure it cannot be found from the UTS by using a yield criterion because that would indeed be for yielding stresses only.

I apologize if the topics here look like a mess, but I feel like I am missing something to connect the dots, because again we have never really gotten in depth in the breaking of a ductile part, only on the yielding. These are questions I have since a few weeks and I checked various books, some about classical strength of materials and some that went deep into theory of plasticity, but they were heavy in math and these problems commonly seem to be solved without having to use such complicated topics, so I wanted to be sure I needed them before studying them.

 

[3DDave]

As the part approaches break, there develops in the most highly stressed area a plateau of stress as the material yields in plastic deformation. This limits the force vs. displacement that is available in the elastic region. As the load increases more and more of the material sees this limit load until the entire section is yielding; a uniform stress field.

One factor to consider is that as the part yields there are many cases where the geometry changes to increase the resistance to load. For example, a horizontal bar, fixed at the ends and a side load in the middle, will bend so that there is a transition from pure shear and bending to tensile loading.

Since geometry is a major factor, it's not reasonable to generalize as to the transfer of such loads.

 

[mfgenggear]

OP
Where to start. There is a lot of talented engineers here. But I will give it a go.
Dave is an experienced engineer.

As a young apprentice I did an apprenticeship
That had me working in every department in a sheet metal and tube shop.
On of those areas was the in house met lab.
I would machine off specimens for micro evaluation and tensile pulls.
From specimens to measure percentage of elongation , yield and ultimate tensile strength.
I had college technical classes as well in metalurgy.
That has been with me through out the years.
In my would which was aerospace gears.
Part of the calculation to verify the right material
Matlab requirements. Tensile strength , wear,
Core hardness for toughness.
While is a long write up and not a direct answer.
In my field we use many formulas by I like to call the fathers of design and manufacture.
Of gears.
The gear root radius is a stress point. And a minimum radius is required to prevent cracking.
I use yield strength plus a safety factor 1.25 min.

 

[rb1957]

"questions about design of mechanical parts so that they don't break"

sorry, everything breaks at some load. You can use semantics such that a component may deflect so much that is no longer functions as expected/required, and say that isn't broken. Sounds pretty broken to me (if it no longer does what is expected of it).

You may be thinking of pressure vessels, with "leak before break". Here the pressure vessel can de designed so that is a small crack develops it will growth stably (not dynamically) and so the pressure vessel will leak pressure (and not explode).

In the sketch you show, experience with common metals shows that the 45 deg line is the critical design feature ... or better, there are methods that combine several ligament lengths (rather than use just the 45deg or the 90deg length). This is because on the 45 deg line the shear is producing tension stresses. And then of course there is bearing to consider.

 

[GregLocock]

Just to add to the complexity the plastic moment method for steel frames actually assumes yield throughout the cross sections that form the hinges. So the structure is still intact, if bent. Similarly the crumple zones on car are designed for post yield integrity.

 

[LittleInch]

It's a big topic here for sure, but I think you're missing the real life issue which is that when something yields it has essentially failed. It might not "break", but it won't be capable of doing what you want it to.

Also may times when something yields, the force dissipates and the yielding stops. If you have a constant load or even worse a shock load then actual breakage is going to happen after you reach yield point.

Your bottom figure would need FEA to figure out where the weak point is.

It does look quite similar to the damage on the toronto plane crash - see the posts here is the Disasters forum. You might learn something from that.

 

[Rocket_Science]

Wow I didn't expect this many answers, thank you for the help! I'll try to answer each of you.

As the part approaches break, there develops in the most highly stressed area a plateau of stress as the material yields in plastic deformation. This limits the force vs. displacement that is available in the elastic region. As the load increases more and more of the material sees this limit load until the entire section is yielding; a uniform stress field.

Ok, this is a thing they taught us. We used the elastic-perfectly plastic model where you assume that the stresses inside the part can reach the yield stress at max, and after that it elongates indefinitely (up until UTS at least).
We also saw a nonlinear FEA result where you could see that this wasn't really the case because of work hardening, and the yielded section had a tensile stress that was higher than the yield stress of the material. This made me wonder if it would be possible to, due to the presence of a particularly nasty notch or fillet, have some part of the section reach UTS and break before the whole section can yield. I asked around and I've been told the topic I was interested in was called "notch sensitivity" of the material. What I concluded after some research is that this could be possible in principle, but common structural steel is way too ductile for this to happen. A teacher told me that the notch geometry required to make this happen is so small that it approaches the domain of fracture mechanics (for ductile steel).

One factor to consider is that as the part yields there are many cases where the geometry changes to increase the resistance to load. For example, a horizontal bar, fixed at the ends and a side load in the middle, will bend so that there is a transition from pure shear and bending to tensile loading.

Since geometry is a major factor, it's not reasonable to generalize as to the transfer of such loads.

Is this the reason why we only studied failure in simple tension? Because it is often enough due to this fact? So the part I've drawn before could behave like in the drawing below?



Here the breaking surface transformed into a straight surface (tension stresses) during yielding. This would explain why we didn't cover breaking with multiaxial stress states.
Still I guess there are some edge cases, maybe that is not always enough. I found a post in these forums that talked about notch strengthening and it was about a notched specimen loaded in tension that failed at a higher load than UTS.
Again I did some research on this topic but I was not very familiar with it. The only useful conclusion I found was that due to the triaxial stress state near the notch, the specimen had a harder time breaking, similarly to how a triaxial stress state makes yielding harder for metals because Von Mises' criterion says that theoretically a ductile metal is not sensitive to hydrostatic stresses.
I still have no idea how to determine if the notch weakens or strenghtens the specimen however because I would need a theory that mathematically describes breaking for that (or physical tests I guess), because the notch could both weaken and strengthen the part apparently.

Part of the calculation to verify the right material
Matlab requirements. Tensile strength , wear,
Core hardness for toughness.
While is a long write up and not a direct answer.
In my field we use many formulas by I like to call the fathers of design and manufacture.
Of gears.
The gear root radius is a stress point. And a minimum radius is required to prevent cracking.
I use yield strength plus a safety factor 1.25 min.

I do remember we had to design some gears for a project involving a gearbox, and we used Lewis' formula for calculating the tooth thickness so that it didn't yield. I do remember we had loads of pages of formulas to use and conditions to verify, many of which didn't seem to have a clear logic behind their derivation. Some, like the bearing stress, were given as a range for a certain class of metals, but there was no logic explained as to why that was the range. My guess is either they were experimental results, or the formula was so convoluted that it was just impractical to use. Even Shigley's book says that for gear design there's a ton of documents due to the difficulty.
In that context we designed by avoiding yielding and by taking into account fatigue as well, so these questions about breaking didn't even cross my mind. As for wear, we didn't really pay that aspect much attention. I was curious and asked the teacher about design of parts by taking into account wear and he said it was a complex and niche topic and that wasn't covered in the course.

Indeed I have a book on wear I want to buy so that I can at least have an idea on what to expect.

"questions about design of mechanical parts so that they don't break"

sorry, everything breaks at some load. You can use semantics such that a component may deflect so much that is no longer functions as expected/required, and say that isn't broken. Sounds pretty broken to me (if it no longer does what is expected of it).

Yes my bad, I didn't specify that I am interested specifically on breaking meant as separation of the part in two or more due to the stresses present inside the part itself due to a static load (no creep, fatigue, wear or corrosion). I was not referring to other conditions like excessive deformations. I think I may have misused the word "break" because I didn't know what word to use to indicate the above, and I didn't want to use the word "fracture" because I associated that with fracture mechanics and in my knowledge that theory is applied only when there is a crack already and you study its propagation.

This is because on the 45 deg line the shear is producing tension stresses.

Do you mean like in a pin hole connection?



I've read that a pin hole can be analyzed as a curved beam, and with that model you mainly have tensile stresses aligned with the beam neutral axis. So the situation described above could be similar to this one here. Also I am ignoring bearing because I didn't think about it when writing the question, but since it is acting on the hole face and there is yielding, it shouldn't affect the two 45° sections, right? It would affect the parts of the sections very close to the hole, but not further away, and stresses should average.

Just to add to the complexity the plastic moment method for steel frames actually assumes yield throughout the cross sections that form the hinges. So the structure is still intact, if bent. Similarly the crumple zones on car are designed for post yield integrity.

This is interesting, I never thought that was the practice. Makes sense since after a crash you cannot allow parts flying around. Is it common in that case to only consider tensile and compressive stresses normal to the beam section? Or are there shear stresses and stresses perpendicular to the beam axis that affect the results?

It's a big topic here for sure, but I think you're missing the real life issue which is that when something yields it has essentially failed. It might not "break", but it won't be capable of doing what you want it to.

Also may times when something yields, the force dissipates and the yielding stops. If you have a constant load or even worse a shock load then actual breakage is going to happen after you reach yield point.

True, in reality that would not be acceptable in any way. It's just that it makes me nervous to not know how to predict the breaking of a part, only the yielding. Like, it makes you feel a bit powerless in scenarios where analysis of these things is required. I've taken a look at Eurocodes 3 and 9 for joint design, and they make you use the UTS of the material for some checks, and that to me looks like an analysis taking into account a state where yielding has already happened and you are trying to prevent the complete breaking of the part.

Your bottom figure would need FEA to figure out where the weak point is.

It does look quite similar to the damage on the toronto plane crash - see the posts here is the Disasters forum. You might learn something from that.

Makes sense, I tried thinking about it but not even considering the detaching part as rigid allows you to approximate the load on each surface, because you would at least need a "buffer thickness" of metal at the surfaces that can deform and produce stresses, but the exact thickness is unknown, and the results depend on it a lot.

As for the Toronto plane crash, I skimmed through the posts and indeed the failure does look similar to the one I drew before. I'll read it in depth these days.

 

[mfgenggear]

I am getting rusty as an OG guy.
For evaluating cycling loads considering
Fatigue. Sn curves is a valuable tool.
Yes Lewis equation. But AGMA standards
Have more robust but conservative formulas
Of the Lewis formulas. Considering Fatigue
Wear. Tooth is a basic beam wear the root radius is the stress point. And is very critical in design.
Here is a link that may answer part of your question what stress loads to use for the number of cycles required to prevent failure or for the minimum cycles.

Siemens Digital Industries Software Community

 

[rb1957]

are we talking fatigue or static failures ? from the OP it sounds like static.

Your sketch shows a hole with a bearing failure ... holes can elongate (thought typically not as much as your sketch !) without failing the part (ie without breaking the part into two).

Things break because the stress in the part exceeds ftu (and other modes too). A local failure (like hole bearing) is sustained because ...
1) the net section stress is less than ftu (a bearing failure shows the stress higher than fty), and
2) the local stress is not so high as to cause dynamic crack growth (ie the material is ductile and has a a high toughness).

 

[mfgenggear]

To determine whether a load is fatigue-related or static in engineering, consider the nature of the loading, its duration, and the material's response. Static loads are constant and sustained, while fatigue loads are cyclic or repeated, potentially leading to material failure over time.

Here's a more detailed breakdown:


1. Understanding the Types of Loads:

• Static Loads:
  These are constant and sustained loads, meaning the magnitude and direction of the load remain the same over time. Examples include the weight of a structure or the force exerted by a stationary object.
  
  
• Fatigue Loads:
  These are cyclic or repeated loads, where the load changes in magnitude and/or direction over time. Examples include the vibrations of a machine, the stresses on a bridge due to traffic, or the force on a rotating shaft.
  

2. Identifying Fatigue vs. Static Failure:

• Static Failure:
  Occurs when a material or structure is subjected to a single load that exceeds its static strength, leading to immediate failure.
  
  
• Fatigue Failure:
  Occurs when a material is subjected to repeated or cyclic loading, leading to crack initiation and propagation over time until failure.
  
  
• Key Differences:
  • Time Dependency: Static failure is instantaneous, while fatigue failure is time-dependent, occurring over many cycles.
    
    
  • Load Type: Static failure is caused by static loads, while fatigue failure is caused by fatigue loads.
    
    
  • Failure Mechanism: Static failure is often characterized by ductile or brittle fracture, while fatigue failure is characterized by crack propagation.
    
    
  • Predictability: Static failure is generally more predictable than fatigue failure, as the material shows signs of yielding or cracking before breaking.
    

3. Factors Influencing Fatigue:

• Material Properties:
  Different materials have different fatigue strengths and resistance to crack propagation.
• Stress Levels:
  Higher stress levels under cyclic loading lead to faster fatigue failure.
• Loading Type:
  The type of cyclic loading (e.g., tension-compression, bending) affects fatigue life.
• Surface Conditions:
  Surface defects or imperfections can act as stress concentrators and initiate fatigue cracks.
• Environment:
  Temperature, humidity, and corrosive environments can accelerate fatigue damage.
  

4. Tools and Techniques for Analysis:

• Static Structural Analysis: Used to determine stresses and displacements under static loads.
  
  
• Fatigue Analysis: Used to predict the life of a component under cyclic loading.
  
  
• Fatigue Testing: Involves subjecting a material or structure to cyclic loading and measuring the resulting fatigue damage.
  
  
• Finite Element Analysis (FEA): A numerical method used to simulate the behavior of structures under various loading conditions, including fatigue.
  
  
• S-N Curves: Graphical representations of the relationship between stress amplitude and the number of cycles to failure, used in fatigue analysis.
  
  
• Rainflow Counting: A technique used to analyze complex stress histories and identify the relevant stress cycles for fatigue analysis.

 

[mfgenggear]

are we talking fatigue or static failures ? from the OP it sounds like static.

Your sketch shows a hole with a bearing failure ... holes can elongate (thought typically not as much as your sketch !) without failing the part (ie without breaking the part into two).

Things break because the stress in the part exceeds ftu (and other modes too). A local failure (like hole bearing) is sustained because ...
1) the net section stress is less than ftu (a bearing failure shows the stress higher than fty), and
2) the local stress is not so high as to cause dynamic crack growth (ie the material is ductile and has a a high toughness).

great point but both should taken in account
like vibration.

 

[mfgenggear]

an other example but not my specialty is aircraft structures vibrations, static and fatigue loads caused by gloads, flexing.
I mean that's all inclusive.

 

[3DDave]

"I wanted to ask some questions about design of mechanical parts so that they don't break"

If they don't exceed the elastic limits then fatigue is the remaining path to failure. Few care about post-yield conditions that lead to failure; some note that localized yielding will offset stress concentrations that do exceed elastic limits.

Components where failure is critical to operation, such as shear pins that ensure sufficient thrust has developed in missile launchers, the is most always done in pure shear with no dependence on elongation.

 

[Rocket_Science]

are we talking fatigue or static failures ? from the OP it sounds like static.

Yes I was asking about static failures specifically. As for fatigue, luckily we had a teacher that is a researcher in that field, so we learned that part well enough (or at least the basics). Still, thank you for the sources about fatigue, mfgengear, I am sure they will be useful for a review of the topic, it never hurts!

Things break because the stress in the part exceeds ftu (and other modes too). A local failure (like hole bearing) is sustained because ...
1) the net section stress is less than ftu (a bearing failure shows the stress higher than fty), and
2) the local stress is not so high as to cause dynamic crack growth (ie the material is ductile and has a a high toughness).

Clearly explained, thank you. So it really makes sense to stop at yielding when analyzing the resistance of a part (excluding cases where resistance has to be guaranteed even after yielding like in the example of crumpled car parts above, but for that the simplification of plastic joints is used, so even then you keep looking at yield stress)

If they don't exceed the elastic limits then fatigue is the remaining path to failure. Few care about post-yield conditions that lead to failure; some note that localized yielding will offset stress concentrations that do exceed elastic limits.

Ok, so if they exceed the elastic limit locally there is low cycle fatigue, if they exceed it in a larger area they have to be redesigned due to what said above.

Components where failure is critical to operation, such as shear pins that ensure sufficient thrust has developed in missile launchers, the is most always done in pure shear with no dependence on elongation.

This last bit is to mean that if there is a part where breaking in two really matters, then they are designed so that breaking happens either due to pure shear or pure tension, so that design, analysis and testing are simpler. Correct?

 

[rb1957]

"So it really makes sense to stop at yielding when analyzing the resistance of a part ..." well, yes, if you want to be super-conservative.

If you want to say your allowable is fty, this is very conservative, but different industries face different challenges. If your material properties are not well controlled (which is expensive) and if your paper trail "isn't" and if the cost of being conservative is acceptable then using a yield allowable would be justified. In my business there is a huge effort put into material properties and traceability and the cost of being conservative is very high then we use ftu as an allowable (because we are very sure that the delivered material will be stronger than this). But then for planes, ftu is rarely a critical failure mode ... most often compression or shear (tension is limited by fatigue concerns).