Usage and Meaning of Direction of Leg Reactions - PLS TOWER

[Trafo1982]

Hi,

I am using PLS TOWER for modeling and designing transmission towers and I notice that they provide two sets of reactions for each support point of the tower model.

They provide customary x,y,z reactions at each support point, but also reactions in Direction of Leg. The TOWER manual appears to show that the two sets are equivalent as the Direction of Leg forces result from an angle transformation of the original x, y, z forces as displayed in the attached image.

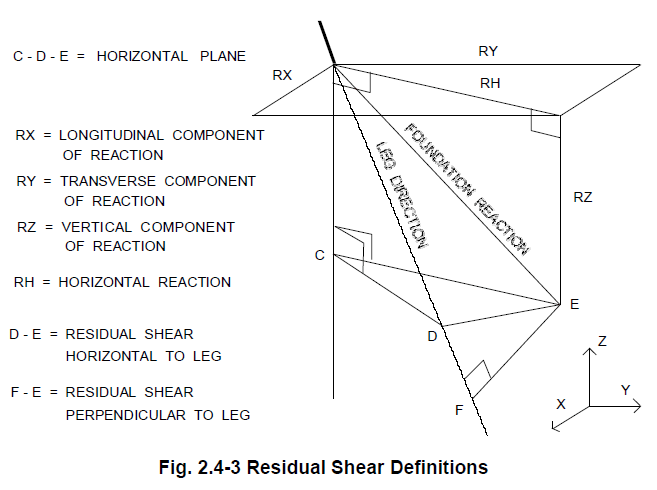
Now, what I notice from the two sets of reactions is a) they indeed produce the same resulting reaction force (sqrt of the sum of the squares), b) they produce a value of axial force along the leg that is larger than the vertical force in the original x, y, z forces, but c) the residual shears produced in the Direction of Leg reaction set are much smaller (15% or less) than the horizontal forces in the original x, y, z set.

My questions:

1. What is the engineering meaning of these residual shears?

2. Is it normal practice to design tower foundations with the Direction of Leg set of reactions?

3. If so, do these residual shears have any use for the design of foundations or they are just neglected when checking stability and bearing capacity? Here I am most concerned about the reduction in the
eccentricity of the loads and their impact in the dimensions of foundations.

Your comments/impressions are much appreciated.

Trafo.

P.S. This is my first post in this forum, so sorry I am missing something in my initial description of the issue.

 

[BAretired]

1. I am no expert on the design of towers, but the reaction at the foundation, R can be resolved into three components, Rx, Ry and Rz. That is all you need to know to design the foundation.

If you are designing the tower leg, you would want to know the axial load and the shear in the major and minor axis in order to determine the moments in the leg about each axis.

I am not clear on the meaning of "residual" shear. The shear, it seems to me, is a result of applied loads, so is not residual by my definition.

2. I would say it is normal practice to design foundations based on the reaction to the foundation, not on the "Direction of Leg" set of reactions.



BA

 

[Agent666]

Based on your picture, the foundation reaction is simply the resultant load vector and its magnitude, i.e. sqrt(Rx^2 + Ry^2 + Rz^2).

The differences between the two systems is that one is in terms of the global coordinates (your Rx/Ry/Rz), the other (the residual ones) are relative/transformed to the local axis of the leg member, these horizontal residuals should be the same as transforming the leg shears/axial loads to the horizontal/vertical planes relative to the leg orientation.

Its a weird way to think about it, but it's simply an alternative way of presenting the exact same loads as the global reactions. You can after all describe these global loads in any number of other coordinate systems, it doesn't change the overall magnitude or direction of the reaction force.

 

[rb1957]

maybe a 3rd time ?

RX, RY, RZ are the leg load in global co-ordinates.

then you have the same leg reaction expressed in local leg axes ... axial (Z?) and two "residual" shear forces (X and Y).
the "interesting" thing about this is the "3rd point" used to define the leg axes is not fixed geometry (as I read your sketch).
It seems to be defining the leg axes system as being along the leg (axial) and then one "residual" shear is the normal vector intersecting the point of the horizontal component; and the other "residual" shear will be orthogonal to these two vectors.
Normally the 3rd point is chosen to make sense for the structural cross-section. But you can always adjust things to suit.

another day in paradise, or is paradise one day closer ?

 

[JLNJ]

Maybe there is some diagonal bracing (not shown) which accounts for the incline of the "foundation reaction".