Vacuum Piston Problem 1

[TheRubberbandMan]

Hello all, I was hoping you could help settle some confusion I have about vacuums.

Suppose I have a perfect piston. It is sealed on one end and exposed to atmosphere on the other. The inside of the piston is a perfect vacuum. For simplicity's sake we'll assume the piston's face has an area of 1 square inch. The seal is perfect, the vacuum is absolute, and the piston is made of an indestructible and rigid material. Now we hang a weight, P, on the piston in an attempt to pull it apart. Below is a crude MS paint drawing I made to illustrate:

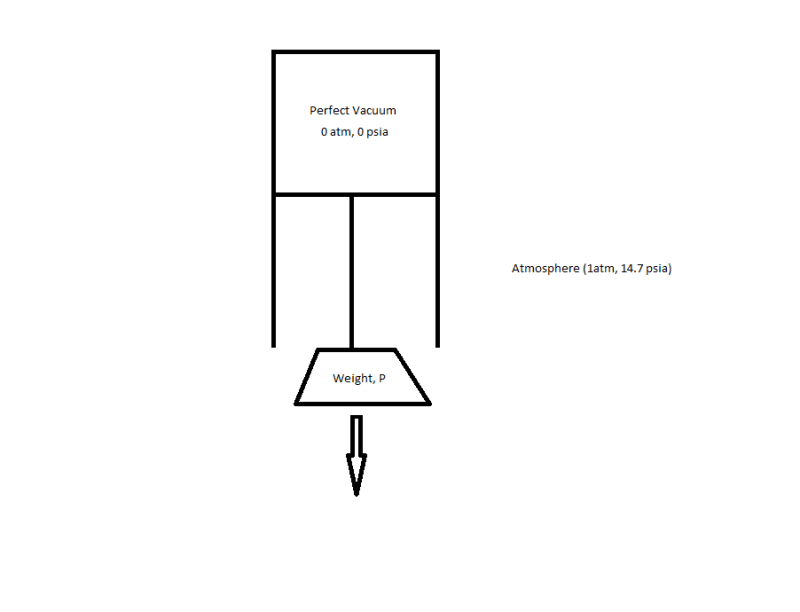
So here is my question: If P is equal to 14.7 lbs (enough to counteract the atmospheric pressure), does the piston slide all the way out? Does it stabilize and then require more weight to pull further? Why?

My thought process here is this: Because the pressure differential cant actually change due to the vacuum being already at absolute zero, the weight would simply counteract the force and slide out with a constant velocity. My colleague believes that pulling this piston apart would get more and more difficult the further you pull it. Who's right?

 

[Compositepro]

You are right. The force stays constant, although the velocity will not. F=ma so acceleration will be constant.

 

[marty007]

+1 to Compositepro

Your colleagues are thinking of a situation where you don't start with a perfect vacuum. If the chamber instead starts at a given pressure (say atmospheric), then as you pull out the piston, the pressure in the chamber will begin to drop. PV=nRT -> P1V1 = P2V2. As the pressure drops, you will need more and more force to pull it out.

However, if you start with a perfect vacuum, then the pressure can't drop any further in the chamber, so the force will remain constant.

 

[chicopee]

If the weight is equal to the counteracting force then there will be no movement of the piston. For movement of the piston the weight has to be greater then force created by the vacuum then you can use F=ma whereby F is the difference in forces.

 

[chicopee]

There is one exception to my above statement and that is if you include the weight of the piston.

 

[LittleInch]

Unless your piston is also magically zero friction, then if your forces balance exactly ( total piston plus weight P = 14.7 lbs, there will be no movement.

As soon as there is even a small difference then the piston will start to move until it either hits the top of the block or comes out of the cylinder.

This is very counter intuitive as pure vacuums don't commonly exist so I can understand your colleagues points, but I agree with the other posters here - you are correct, but the velocity won't be constant.

Remember - More details = better answers
Also: If you get a response it's polite to respond to it.

 

[TheRubberbandMan]

Thank you everyone! This has been very informative.