Validating Equations for Excel Against Typo's/Formatting Errors 2

[racookpe1978]

Self-study for PE "continuing ed" credits evaluating a lot of obtuse scientific data from different papers.
Data is varying across day-of-year (0-365) , time-of-day (24 hours), or latitide (90 degrees).

Anything I can type, I can type incorrectly. Anything cell I can link to, I can link to incorrectly. Etc.

I need to check that the equations I've developed to approximate the data points are are right: but that they are also "right" across the data.

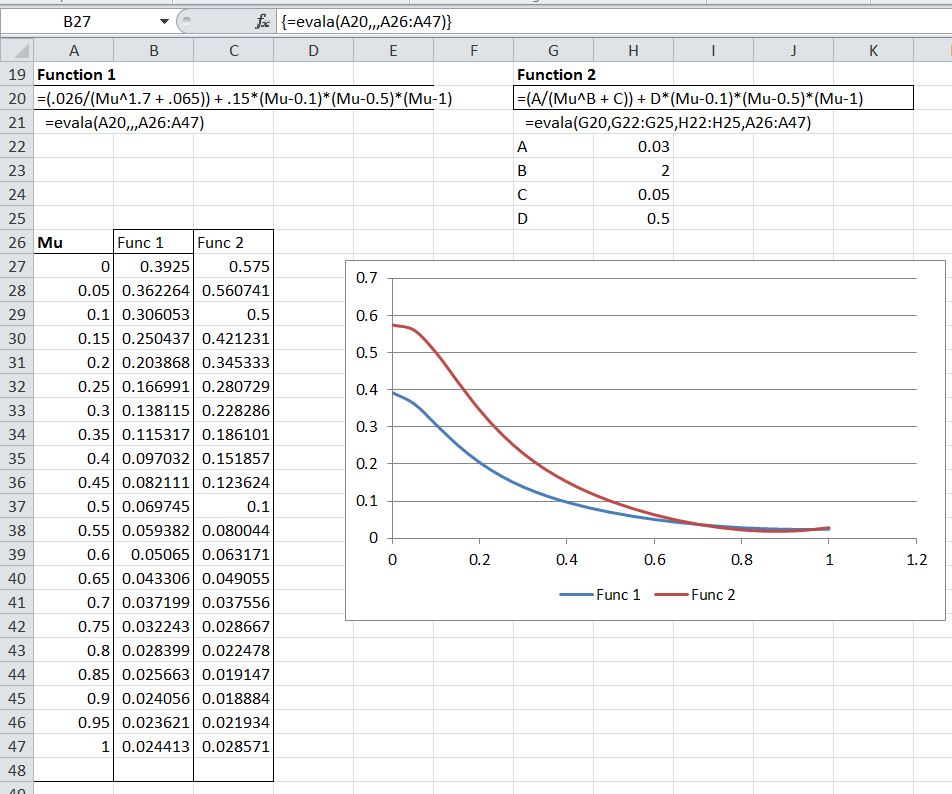
Is there any way to plot an equation in Excel - without making a 365 cell-by-cell "plot" of all of the data points? Now classically, you create a spreadsheet with data points in two columns, then make a graph. But can you display an equation (a sine wave for example) over a range of values without having to create the data table?

If no, And I think that is what I will find, is there a compatible graphics program that can do this function? Ideally, I'd like to verify the equation, then copy-and=paste it into Excel.

 

[IDS]

If no, And I think that is what I will find,

But the answer is yes.

See:

http://newtonexcelbach.wordpress.com/2010/12/15/charting-a-mathematical-function-with-defined-names/

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[electricpete]

Doug answered the question well. By the way he has a great website with lots of useful goodies for excel.

I'm trying to step back to understand how the particular request fits in with your stated goal and I can't quite get there. You have developed a (long, complicated?) expression F(X,Y,Z) to approximate the data and you want to validate it against existing graphs (by generating similar graphs) and perhaps use it in other ways without making typo's..

I think I would code the function in just once as a user-defined vba function of the three variables. That will help minimize the typographical errors in applying the function repeatedly in different scenario's.

Plot of a function against three independent variables is a challenge (unless you use surface/contour plot, which I'm not necessarily recommending). So I imagine you want several plots, changing the independent variables and changing the ranges. In addition to approach at Doug's site, you can also tailor your graphs for each change of the independent variables by clearly separating the independent variables in columns on left side and rows along the top... each built by adding a "delta" to the previous value. Then you can easily rescale that independent variable by changing the starting value and the delta.



=====================================
(2B)+(2B)' ?

 

[electricpete]

Correction:

In addition to approach at Doug's site, you can also

should've been:

As alternative to approach at Doug's site, you can also

In other words I was suggesting an alternate (more traditional / obvious) approach that I thought might be easier than plugging named formula's into your graph (which is quite elegant, but maybe a little tricky to learn). Whatever works for you.. it's good to have alternatives.

=====================================
(2B)+(2B)' ?

 

[racookpe1978]

Yes. Boy, that was informative, wasn't it? /self-rhetorical questioning mode. 8<)

For example:
I am trying to be consistent in my notes and in all of the other plots of using "solar elevation angle" SEA as a primary input
SEA = = 90-solar zenith angle.
In one paper (referenced by several others) Mu is the "cos of solar zenith angle" (I am already three steps away from my original definition away from solar elevation angle.)
Then albedo (which is what I am look for relationships around, above, below and between all these different papers) is said to be = (0.026/(Mu^1.7 + 0.065)) + 0.15*(Mu-0.1)*(Mu-0.5)*(Mu-1.0)

Several other papers (dating back to the 1950's) have only paper-plots of albedo vs solar zenith angle, and others have albedo vs solar zenith angle. No equations at all -> Have to print the graph, paper-read the dots and circles, type in the points, and back-generate a polynominal or other curve of some sort that might fit. Or might not fit. Then compare those curves against the paper-plot points, against the Mu-equation curve, etc. Etc. Etc.

So what is supposed to be the heat transfer rate as solar elevation angle changes? Obviously, first I need to get everybody's data and equations on one plot at one time to see what matches and what duplicates data ranges and what stops too short or is too limited. and, what equations might simply completely wrong. I know already that the "ideal" Fresnel reflection equation for light from "perfect water" does NOT match the measured data fro the open ocean. But the Fresnel equations themselves are a nightmare to check for typo's. 8<)

That's what i meant by saying that it's almost impossible to "audit" any resulting calculations: I can't "look at " the even the first results of any given line or column in the spreadsheet to look at those values and see if they make sense without first plotting the results to see if what i typed is correct.

I'm going to pull up the references above and continue the process.

 

[racookpe1978]

Single typing equations at the top of a sheet once?
Absolutely the right way to go. (Compared to repeating an equation in an entire column of relative-referenced cells?)

But, typing the equation once using a mix of fixed references $r1$c1 and fixed and relative references $r1c1? How do you repeat that equation when you have many different sheets? Defining a constant (Mu for example using the equation above) sets that one value of Mu for the entire spreadsheet, which does not allow you to use a different Mu on each of 32 different sheets.

Or, writing one equation one time on the first sheet requires somehow linking different sheets back to the first sheet for some variables, and resetting variables for others based on row and column designations. In either case, the fundamental equation gets longer and the probability of incidental errors becomes a near-certainty. And, worse, the ability to find out that there IS an error becomes almost impossible if the introduced error is because a variable is NOT being updated properly on one sheet due to a "lock" or rewrite of that variable by a very-close-but-not-right-value on a different sheet.

tricky, right?

So, my hope was to be able to type out different very complex equations quickly and almost immediately "look at" the results over a data range. This is to see if there are errors from what I expect based on the original graph in some paper-copy article. Change a value, and check again to see if the results continue to make sense. (It should be hotter in July than in May, for example. Albedo should increase as solar angle gets larger. Albedo should never be lower than 0.06 over all data ranges from 0 to 90 degrees. Albedo should never be greater than 1.00 for all data ranges. There should never be a sudden "jump" or dip in albedo as solar angle increases, etc.

 

[electricpete]

So, my hope was to be able to type out different very complex equations quickly and almost immediately "look at" the results over a data range. This is to see if there are errors from what I expect based on the original graph in some paper-copy article

For this particular thing, the approach recommended by IDS is pretty good. I have attached a spreadsheet based on similar results. It has pre-defined parameters up top, which can easily be changed. The function y, z, u, v can easy be edited in terms of independent variable and parameters and display is instantanous. I think it's built on similar approach as Doug's. His was a parameteric example (x(t), y(x)), this is using one independent variable x. It would represent whatever independent variable you happen to be examining at the time.

As far as the rest, I'm not sure what the unifying theme of the request is. fwiw my first thought about how I would approach (based on my limited understanding of the task) is to build one tab per article. Then build my model right next to it in the same shet. Then use chart wizard to plot the results and keep plot embedded in the sheet along with the input variables and notes. How to prevent overlapping of variables which have similar/same names in different sheets is a bit of a challenge. There are scoping rules which can be used to take care of it, but I'd be inclined to never use the same name for something that has different meaning in different sheets. Perhaps put a suffix or prefix onto the variable to denote which project (sheet) it goes with. Another approach if each analysis is too complex to fit in a tab is to build one spreadsheet per article... gets a little trickier navigating among reuslts then.



=====================================
(2B)+(2B)' ?

 

[electricpete]

I have attached a spreadsheet based on similar results

Sorry, attached now to this post.

Regardless of whether you start with my spreadsheet or Doug's, you're obviously going to have to modify the structure somewhat to get what you want. In that sense, Doug's is probably a better starting point because he explained exactly how his is built

=====================================
(2B)+(2B)' ?

 

[racookpe1978]

Got it. Will work on it sum more manana. 8<)

 

[IDS]

Looking at what you want to do in more detail, I think my EValA function would be better for your purposes than using named formulas in charts. The screenshot below shows the output from this function with two versions of your function:
=(.026/(Mu^1.7 + .065)) + .15*(Mu-0.1)*(Mu-0.5)*(Mu-1)
=(A/(Mu^B + C)) + D*(Mu-0.1)*(Mu-0.5)*(Mu-1)

In both cases the Mu values, over the range you want to plot are listed in a vertical range, with "Mu" at the top.
For the second you also need a column with the parameters listed (A, B, C, D) and the corresponding values (I've changed the values you gave, just to plot a different line).

Unlike using named ranges, you can use the same parameter with different values anywhere in the workbook, even on the same sheet. There are a couple of points you need to be aware of.

The function needs to be entered as an array function:
- Enter the function (or copy and paste) in the top cell.
- Select the entire output range (including the top cell).
- Press F2, then Ctrl-Shift-Enter

If your function includes named functions (such as sin or cos), you need to make sure your parameter names do not appear in the function names. Easy ways to do this are to use entirely upper case for the parameters, and lower case for the functions, or terminate all parameters with a _.

A spreadsheet including the function is attached (including the example shown above). If you have any problems with it, please ask.

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[racookpe1978]

Way cool!