James B
Geotechnical
- Aug 20, 2021
- 3
Hi All,
I have recently come across a new request in my practice. A structural engineer has requested a lateral soil spring for a shallow (both concrete pad [not mat or raft] and steel grillage) foundation. I have provided vertical soil springs for raft/mat foundations and lateral soil springs for deep foundations many times but have never been asked for either for a small spread footing. When I query the structural on why this is required he needs it as a "program input" - which is my first red flag - he does not understand what the parameters are or how they are used.
Regardless, I am confident in providing a vertical subgrade modulus using Winkler and Terzhagi methods for a spread footing by the equation of Kz = Qa/S. In my case we have about firm soils (silty clay) with an undrained shear strength of 50 kPa, an allowable bearing capacity of 50 kPa and the structure's allowable settlement is 25 mm = a very simple result of Kz = 50 / 0.025 = 2 MN/m3.
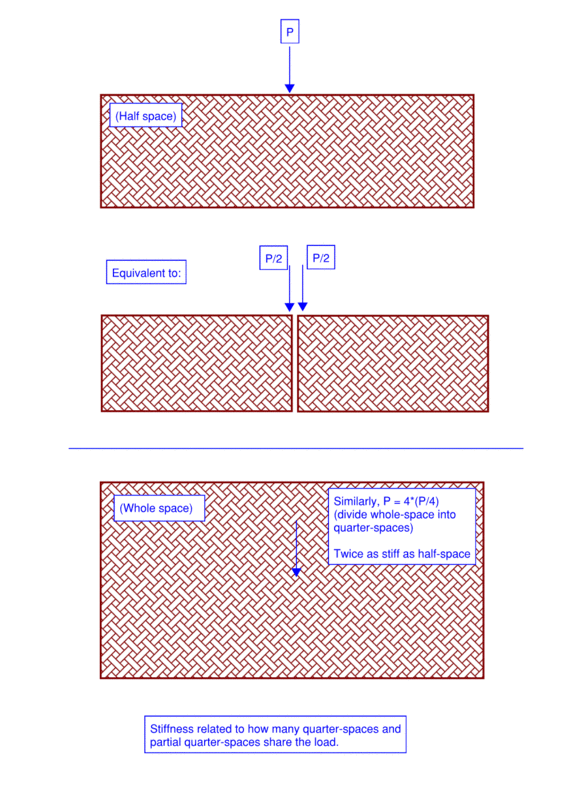
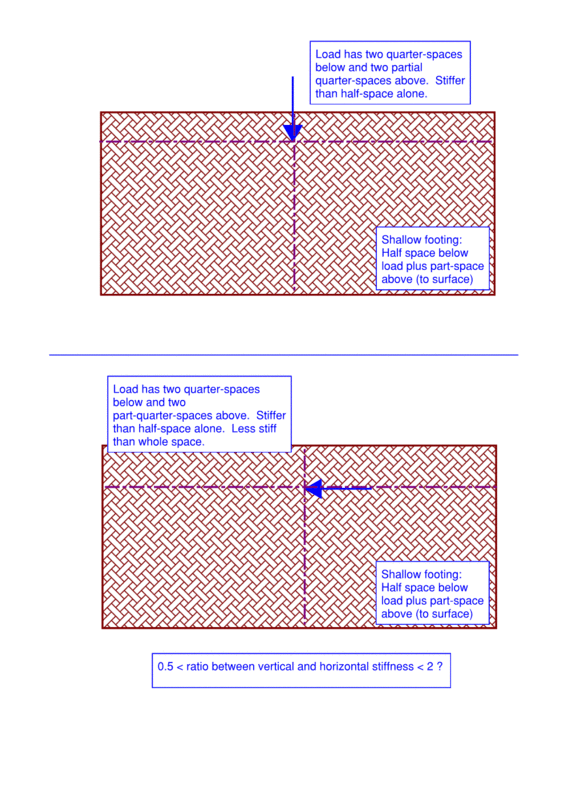
For the lateral modulus I am at a loss of how to interpret this by hand or other methods. I have tried finding papers and only come across an ASCE paper that indicates the lateral modulus may be obtained by Kh = 2Es/b. In my case I have assumed an Es = 10 MPa (firm silty clay) and b = 1.5 m (foundation dimension) which results in Kh = 13.3 MN/m3. This is 6x the vertical modulus and clearly something is missing in this equation, unless I have severely overestimated the Es which should be 3 MPa and this seems unreasonably low for a material with an Su = 50 kPa. Is there any guidance on lateral modulus for shallow foundations?
I also understand that typically lateral modulus is 1.5 - 2x higher than vertical, I just can't seem to find a paper that can justify this to provide to the structural engineer as backup documentation.
I have recently come across a new request in my practice. A structural engineer has requested a lateral soil spring for a shallow (both concrete pad [not mat or raft] and steel grillage) foundation. I have provided vertical soil springs for raft/mat foundations and lateral soil springs for deep foundations many times but have never been asked for either for a small spread footing. When I query the structural on why this is required he needs it as a "program input" - which is my first red flag - he does not understand what the parameters are or how they are used.
Regardless, I am confident in providing a vertical subgrade modulus using Winkler and Terzhagi methods for a spread footing by the equation of Kz = Qa/S. In my case we have about firm soils (silty clay) with an undrained shear strength of 50 kPa, an allowable bearing capacity of 50 kPa and the structure's allowable settlement is 25 mm = a very simple result of Kz = 50 / 0.025 = 2 MN/m3.
For the lateral modulus I am at a loss of how to interpret this by hand or other methods. I have tried finding papers and only come across an ASCE paper that indicates the lateral modulus may be obtained by Kh = 2Es/b. In my case I have assumed an Es = 10 MPa (firm silty clay) and b = 1.5 m (foundation dimension) which results in Kh = 13.3 MN/m3. This is 6x the vertical modulus and clearly something is missing in this equation, unless I have severely overestimated the Es which should be 3 MPa and this seems unreasonably low for a material with an Su = 50 kPa. Is there any guidance on lateral modulus for shallow foundations?
I also understand that typically lateral modulus is 1.5 - 2x higher than vertical, I just can't seem to find a paper that can justify this to provide to the structural engineer as backup documentation.