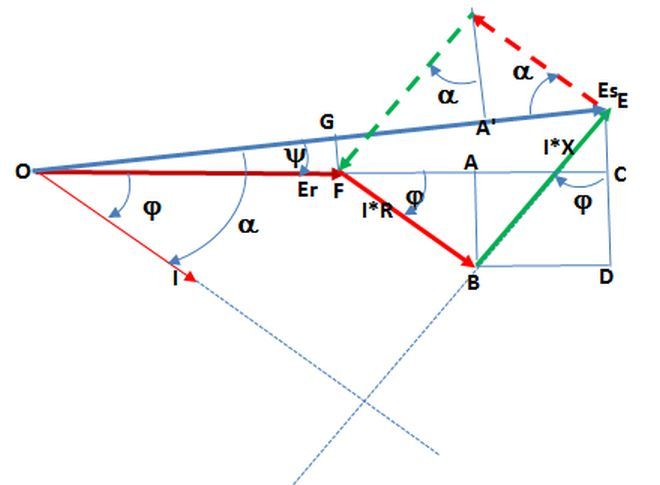
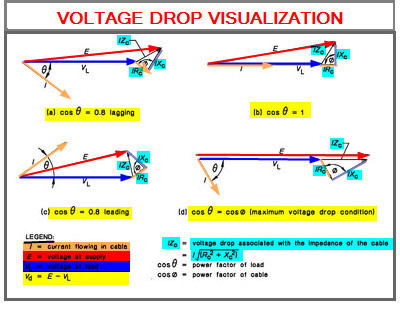
1. In voltage drop calculations the Voltage drop equation is IR Cos (phi) + IX Sin (phi). What is phi here?
Phi - Power factor angle of the load
(or)
Phi - Internal Impedance angle of the transformer (arc tan (X/R)) where X/R is the X/R of the transformer.
2. For example, In cable size adequacy check, Phi is the load power factor angle, not the arc tan (X/R) of the cable. Here why not the cable angle is considered?
3. Is voltage drop at full load due to %Z is same as the voltage regulation? what is the difference between as it appears to be the same? How power factor affects the voltage regulation?
Phi - Power factor angle of the load
(or)
Phi - Internal Impedance angle of the transformer (arc tan (X/R)) where X/R is the X/R of the transformer.
2. For example, In cable size adequacy check, Phi is the load power factor angle, not the arc tan (X/R) of the cable. Here why not the cable angle is considered?
3. Is voltage drop at full load due to %Z is same as the voltage regulation? what is the difference between as it appears to be the same? How power factor affects the voltage regulation?


![[pipe] [pipe] [pipe]](/data/assets/smilies/pipe.gif)