Which Section Modulus do you use for Minor Axis Bending of Channel? 1

[anchorengineer]

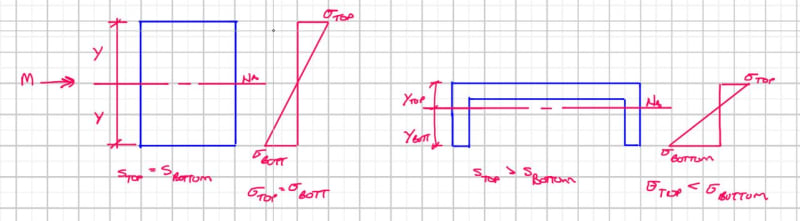
We typically use the the weaker of the section modulus for minor axis bending of a channel (Syy -X vs Syy +X), but is that overly conservative? Can someone point me to a good reference to back this up?
Thanks!

 

[Lomarandil]

Is your controlling limit state tensile or compressive?

If your channel orientation and load direction are consistent, no reason you can't take advantage of the appropriate section modulus.

 

[rb1957]

be conservative, but have your eyes open.

using minimum section modulus is conservative (or realistic if the load is aligned).
if this assumption causes you grief (maybe as a result of reworking the design, and you're trying to show the design is good) then revise to the realistic analysis.

"Hoffen wir mal, dass alles gut geht !"
General Paulus, Nov 1942, outside Stalingrad after the launch of Operation Uranus.

 

[Celt83]

Limiting the discussion to only yielding as a limit state.

Remember from mechanics of materials that for a linear elastic material and from Hooke's Law --> σ = M*y / I
where y is the distance measured from the elastic neutral axis to the location of interest.

When y is the maximum distance to the cross-sections extreme fiber then y / I = 1 / S or I / y = S, where S is defined as the elastic section modulus. When a shape is symmetric the distance from the elastic neutral axis to either extreme fiber is the same and S,top = S,bottom, and by extension σ,top = σ,bottom. When the cross-section is not symmetric as is the case with a channel in weak axis bending S,top ≠ S,bottom, and σ,top ≠ σ,bottom. If the channel is oriented such that the flanges face down then S,top > S,bottom and σ,top < σ,bottom meaning that σ,bottom would be the controlling stress for yield.

 

[JStephen]

In the ASD AISC, weak-axis bending is just given as a maximum stress without regard to whether it's compression or tension, for bars and W-sections.
Channels aren't addressed at all that I see, but would presumably fall under the same category. So allowable tension=allowable compression, and you'd use the minimum if that was the only criteria.

 

[phamENG]

Check out Section F6 in AISC 360.

S[sub]y[/sub] = elastic section modulus taken about the y-axis, in.[sup]3[/sup]; for a channel, the minimum section modulus.

 

[Lomarandil]

Oh, interesting Pham. My 15th edition has a check for flange local buckling (if noncompact or slender), which I would only apply to the compression side section modulus. The Sy definition in that edition doesn't talk about it being the minimum section modulus.

That said, there's a big grey note saying that no modern channel section at 50ksi is noncompact, so it might only apply to those of us working with historic shapes.

 

[phamENG]

I'm cheap - I still haven't upgraded my text copy, and I reach for it more than I search a PDF.

 

[ProgrammingPE]

As Celt83 mentioned, the lower Sy will give you the stress at the tip of the flanges and the higher Sy will give you the stress at the web. The stress will be higher at the tip of the flanges since it has a lower Sy and σ = M/S. (The Dimension and Properties tables in Part 1 of the Steel Construction Manual only list the lower Sy value.)

For the Yielding check, the maximum stress anywhere in the shape is what is critical since that is where yielding will initiate, so you use the lower Sy.

For the Flange Local Buckling check, the maximum stress in the flange will be at the toe of the flange, which can be determined using the lower Sy.

I would suspect, though, that the Flange Local Buckling check is only accurate when the toes are in compression. Flange Local Buckling occurs due to compressive stress, and when the toes are in tension, the compressive stress in the flange is only in the region that is right next to the web which braces the flange. (The compressive stress for this case would also be determined using the higher Sy.)

This issue of checking buckling of unsymmetrical shapes also comes up for Single Angles which only check buckling when the toes are in compression (F10.3), for Tees which only check Local Buckling of Tee Stems when the stem is in compression (F9.4), and for Tees which only check Flange Local Buckling when the flange is in compression (F9.3). (The Flange Local Buckling check for Tees actually adds a Sxc variable for its check instead of Sx to make it clear that the higher S value gets to be used.)

Structural Engineering Software:

http://www.structuralcentral.com/tools/steel-connection

Structural Engineering Videos:

http://www.youtube.com/structuralcentral

 

[rb1957]

I assumed the OP was using the highest stress (magnitude) from the lowest section modulus as either tension or compression.

"Hoffen wir mal, dass alles gut geht !"
General Paulus, Nov 1942, outside Stalingrad after the launch of Operation Uranus.