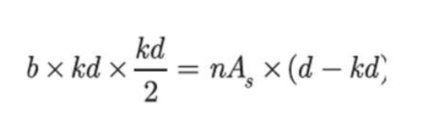canadiancastor
Structural
- Apr 13, 2014
- 37
I'm having a look at some formula I use all the time and wondering why two things I'm calling the neutral axis appear to be different things. Or maybe there's a simplification that we're doing that I don't quite understand.
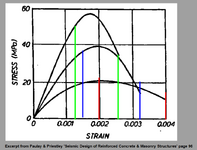
In the first example, we are looking at strain, then stress, then finding a balance between compresion and tension forces.
In the second example, we are looking at simply the areas * lever arm of compression vs tension and balancing those. This is quite different than number 1, specialy if you have a triangular distribution of strain in the concrete (low stress).

The actual question behind this is that if serviceabillity is always in the elastic range, shouldn't we assume that the concrete has a triangular strain and stress distribution? If so, would we not need to take the lever arm about the center of gravity of the triangle (2/3 * c) and the area of the triangle as 1/2 of the rectangular area? This would be akin to what is done in the ultimate moment determination of the neutral axis.
In the first example, we are looking at strain, then stress, then finding a balance between compresion and tension forces.
In the second example, we are looking at simply the areas * lever arm of compression vs tension and balancing those. This is quite different than number 1, specialy if you have a triangular distribution of strain in the concrete (low stress).

The actual question behind this is that if serviceabillity is always in the elastic range, shouldn't we assume that the concrete has a triangular strain and stress distribution? If so, would we not need to take the lever arm about the center of gravity of the triangle (2/3 * c) and the area of the triangle as 1/2 of the rectangular area? This would be akin to what is done in the ultimate moment determination of the neutral axis.