Hello,
Hope there's a spline guru out there who can help me with this. I have found it very convenient to sketch splines and define them using tangents and tangent weighting (SW2014), but for my numerical analyses I need to have the representative polynomials. I can manually brute-force this using points measured in SW and interpolating, but if the two sets of parameters define the same curve, there should be an underlying translation formula which I can use? (I'm not familiar with exactly what "tangent weighting" is in a mathematical sense, and I've unfortunately been able to find but little on the subject.) Example below.
Many thanks in advance.
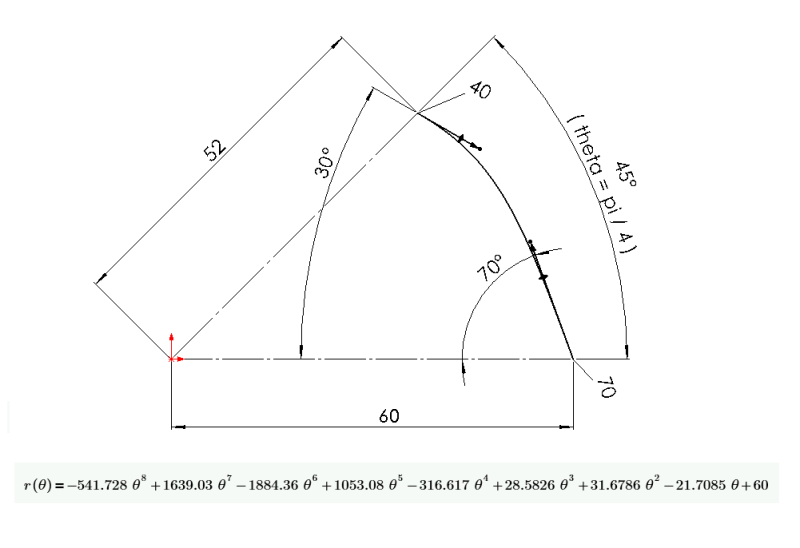
Hope there's a spline guru out there who can help me with this. I have found it very convenient to sketch splines and define them using tangents and tangent weighting (SW2014), but for my numerical analyses I need to have the representative polynomials. I can manually brute-force this using points measured in SW and interpolating, but if the two sets of parameters define the same curve, there should be an underlying translation formula which I can use? (I'm not familiar with exactly what "tangent weighting" is in a mathematical sense, and I've unfortunately been able to find but little on the subject.) Example below.
Many thanks in advance.

