Dear All,
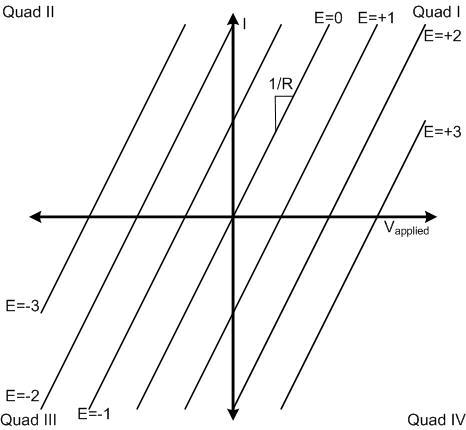
My background is mechanical and I was looking to understand the theory of regenerative braking in DC motors. I found this article online In Figure 3, it shows that in braking quadrants 2 and 4 there is regeneration space which you can regenerate energy within this space only and you need to apply voltage outside this space in quadrant 2 and 3 to brake or slow down the load.
I am wondering if there is textbook explain these issues and their theories. I only find this article and I looked for many textbook, but I couldn't find detail explaination of this point. Can you recommend me a textbook. I need urgently.
Thanks in adavance
My background is mechanical and I was looking to understand the theory of regenerative braking in DC motors. I found this article online In Figure 3, it shows that in braking quadrants 2 and 4 there is regeneration space which you can regenerate energy within this space only and you need to apply voltage outside this space in quadrant 2 and 3 to brake or slow down the load.
I am wondering if there is textbook explain these issues and their theories. I only find this article and I looked for many textbook, but I couldn't find detail explaination of this point. Can you recommend me a textbook. I need urgently.
Thanks in adavance