ColinPearson
Petroleum
- May 1, 2011
- 142
Hello folks!
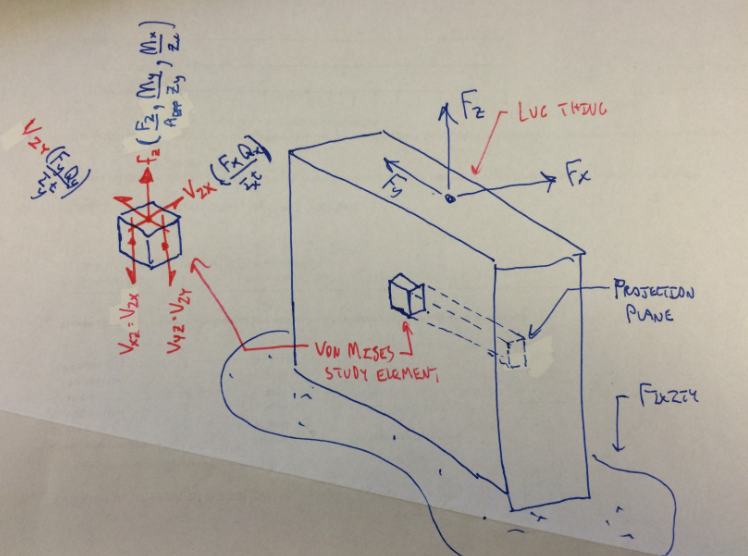
It's been a long day in an already very long week and it's only Monday so maybe some sleep would help, but I have a question about ASME BTH-1-2014 Eq 3-37. It's turned up before on the forum but not really in a way that answers my questions. Really, I think I jsut need a little hand-holding here...
fcr = SQRT( fx^2 - fxfy + fy^2 + 3fv^2) <= Fy / Nd EDIT: original post said "+ fxfy", fixed here
where:
fx = computed normal stress in X direction
fy = computed normal stress in Y direction
fv = computed shear stress
Now... say my XY plane is "flat", and I've got forces Fx, Fy and Fz. Let's say further that all forces act at some moment arm such that there are bending stresses induced by all three forces. Now, I would consider the compression and tension resulting from those bending stresses to be acting normal to the XY plane, but wouldn't you say they acted in the Z direction? I'm confused when the explanation of the variables offered by ASME talks about the normal stresses in both the X and Y directions; do they mean the normal stresses caused by the forces acting along X and Y? I'm looking at BTH-1-2014 Chapter 3-2.5; same chapter for the 2011 version.
Thanks in advance, cheers! (sketch attached)
It's been a long day in an already very long week and it's only Monday so maybe some sleep would help, but I have a question about ASME BTH-1-2014 Eq 3-37. It's turned up before on the forum but not really in a way that answers my questions. Really, I think I jsut need a little hand-holding here...
fcr = SQRT( fx^2 - fxfy + fy^2 + 3fv^2) <= Fy / Nd EDIT: original post said "+ fxfy", fixed here
where:
fx = computed normal stress in X direction
fy = computed normal stress in Y direction
fv = computed shear stress
Now... say my XY plane is "flat", and I've got forces Fx, Fy and Fz. Let's say further that all forces act at some moment arm such that there are bending stresses induced by all three forces. Now, I would consider the compression and tension resulting from those bending stresses to be acting normal to the XY plane, but wouldn't you say they acted in the Z direction? I'm confused when the explanation of the variables offered by ASME talks about the normal stresses in both the X and Y directions; do they mean the normal stresses caused by the forces acting along X and Y? I'm looking at BTH-1-2014 Chapter 3-2.5; same chapter for the 2011 version.
Thanks in advance, cheers! (sketch attached)