Hello Everyone,
I hope I am posting my question in the right place.
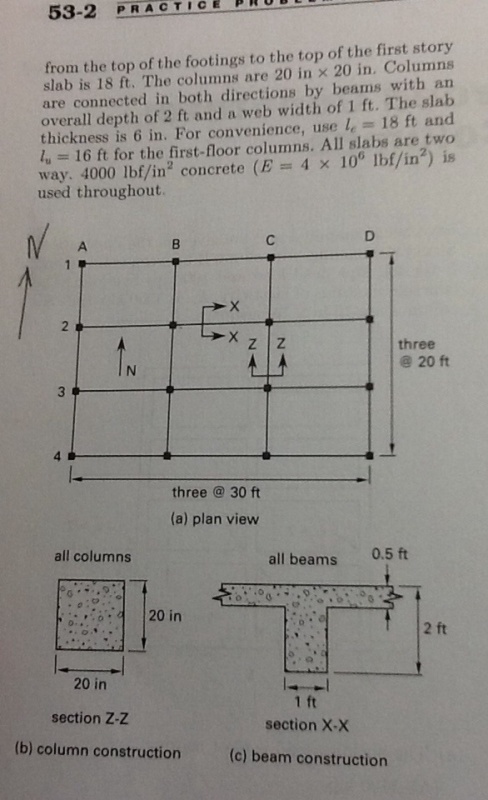
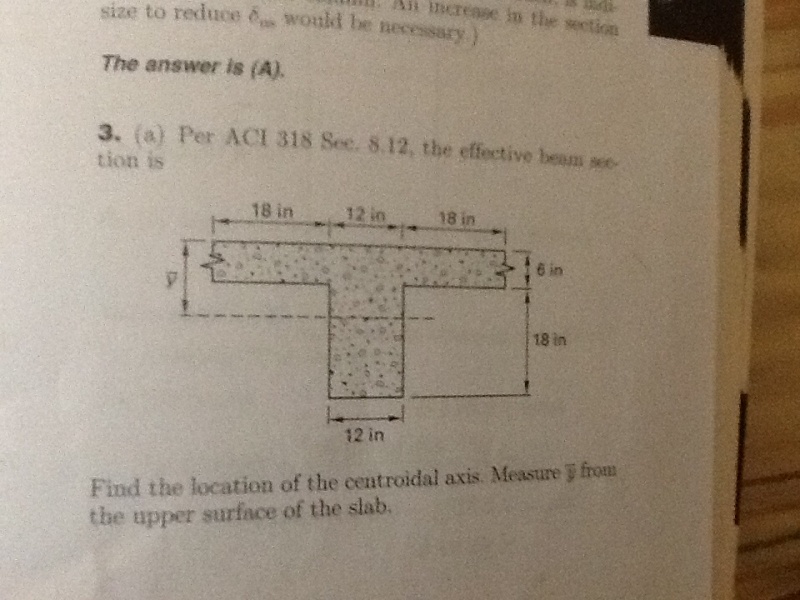
I am solving a problem in Linderburg for reinforced concrete slender column chapter. He is using in one of the questions a two way slab- t beam with the effective flane width unknown. Per aci 8-11, the effective flange width shall be minimum quarter span etc... However, he is determining the value based on isolate beam criteria. I don't quite understand why. I am thinking of isolated beam in a literal sense as it is isolated unless there is something I do not understand. I will truly appreciate if someone can clarify to me why he is using isolated beam criteria. I know this might be simple for many but not for me yet.
Thanks a lot.
I hope I am posting my question in the right place.
I am solving a problem in Linderburg for reinforced concrete slender column chapter. He is using in one of the questions a two way slab- t beam with the effective flane width unknown. Per aci 8-11, the effective flange width shall be minimum quarter span etc... However, he is determining the value based on isolate beam criteria. I don't quite understand why. I am thinking of isolated beam in a literal sense as it is isolated unless there is something I do not understand. I will truly appreciate if someone can clarify to me why he is using isolated beam criteria. I know this might be simple for many but not for me yet.
Thanks a lot.