Hi all,
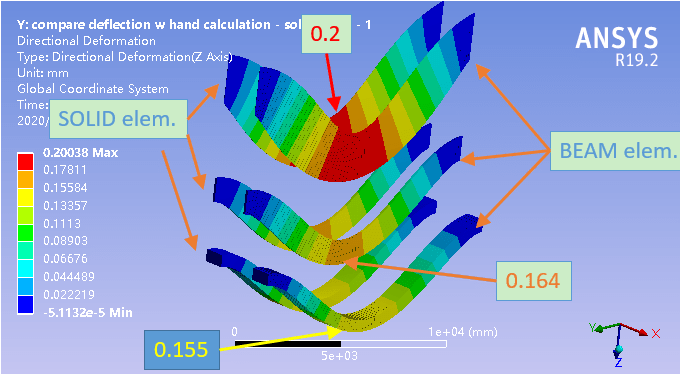
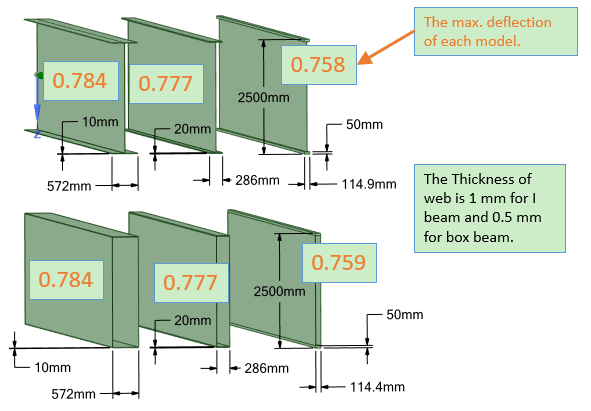
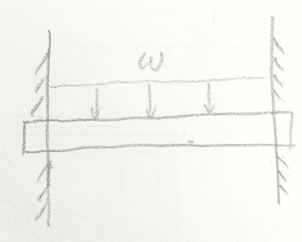
Does anyone know why different deflection is obtained when the moment of inertia is identical? The following beam and solid all have the same moment of inertia along the global X axis. The load is a uniformly force on top of each model and all 6 DOFs of all the beams are constrained at both ends (for solid the 3 translational DOFs are constrained.)
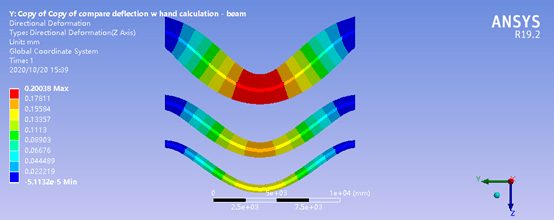
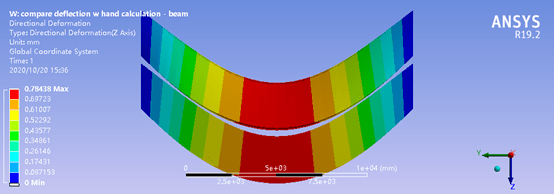
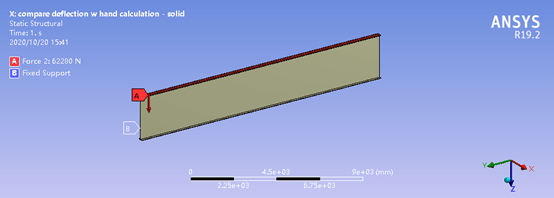
The max. deflection w/ hand calculation is 0.152 mm which is very close to the model w/ cross section of width=1000mm and height of 600mm.
The web of I beam and box beam is very thin, i.e. 1 mm.
Thanks in advance!
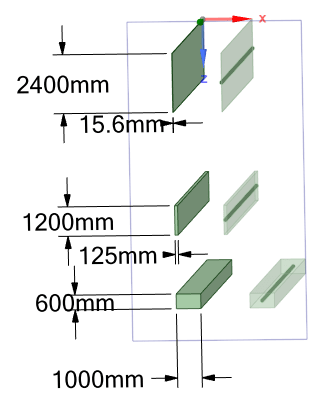
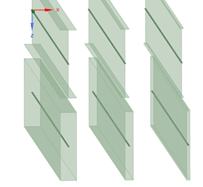
Does anyone know why different deflection is obtained when the moment of inertia is identical? The following beam and solid all have the same moment of inertia along the global X axis. The load is a uniformly force on top of each model and all 6 DOFs of all the beams are constrained at both ends (for solid the 3 translational DOFs are constrained.)
The max. deflection w/ hand calculation is 0.152 mm which is very close to the model w/ cross section of width=1000mm and height of 600mm.
The web of I beam and box beam is very thin, i.e. 1 mm.
Thanks in advance!