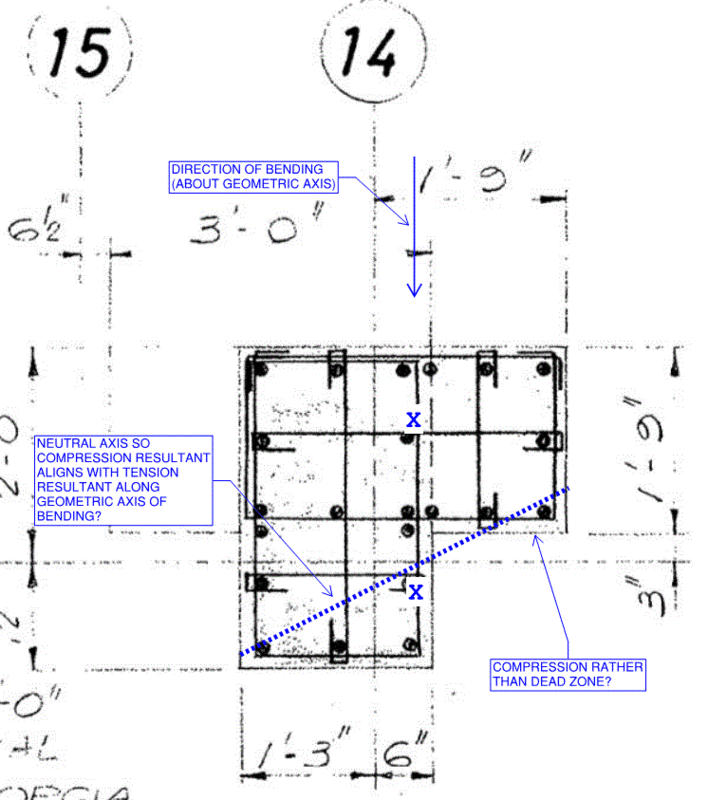
Good Afternoon,
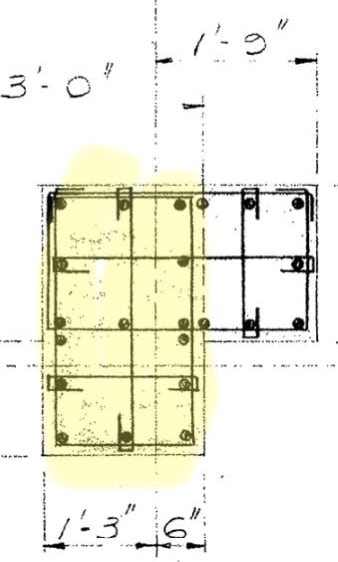
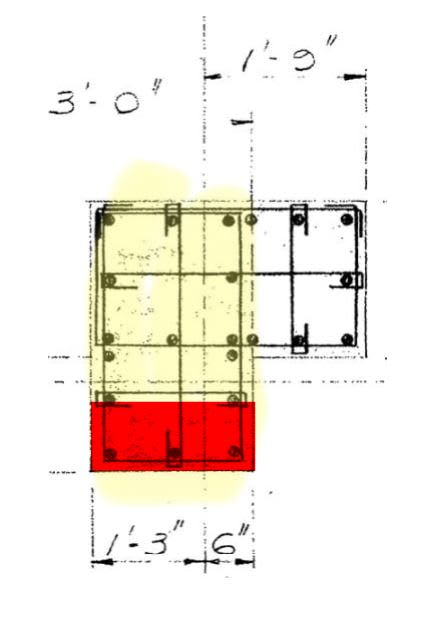
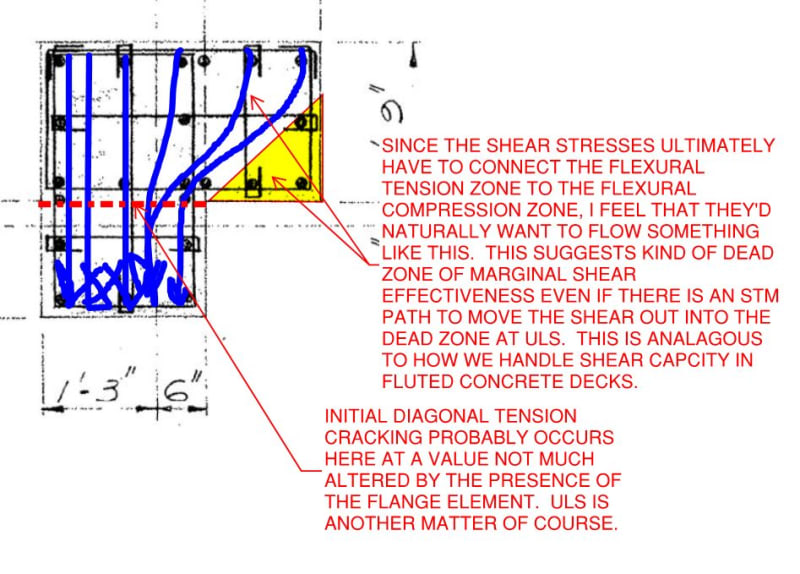
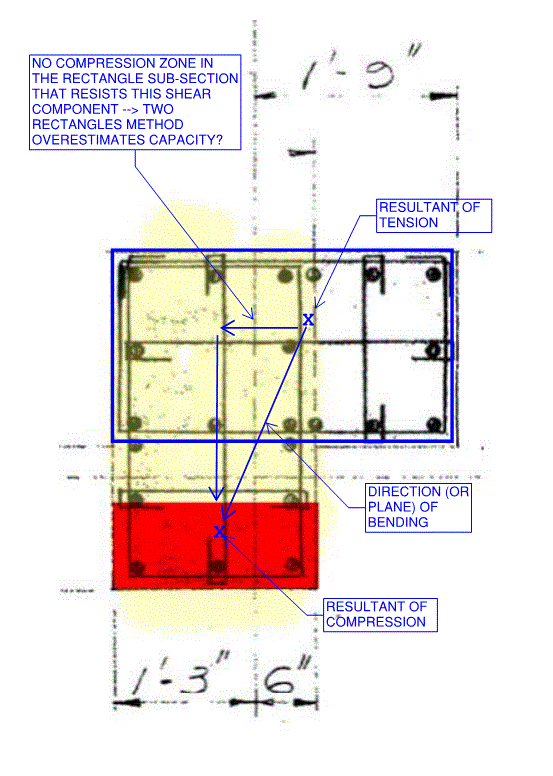
I am doing some checks for shear strength of columns in an existing building and have come across several L-shaped columns. I can think that I could check these like i might check shear strength of an L-Shaped beam, but this would end up being very conservative, and I need my values to be fairly accurate. Does anyone have any resources or thoughts on an approach to calculating shear strength of a column like this?
Thank you so much for your time!
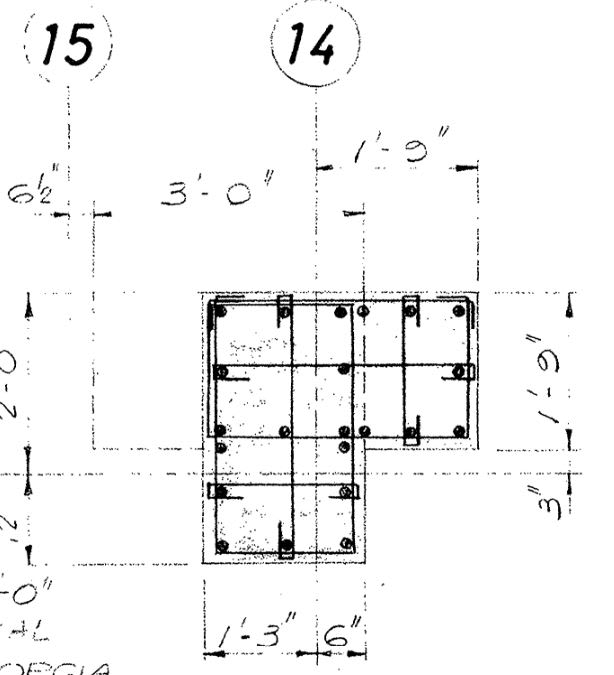
I am doing some checks for shear strength of columns in an existing building and have come across several L-shaped columns. I can think that I could check these like i might check shear strength of an L-Shaped beam, but this would end up being very conservative, and I need my values to be fairly accurate. Does anyone have any resources or thoughts on an approach to calculating shear strength of a column like this?
Thank you so much for your time!