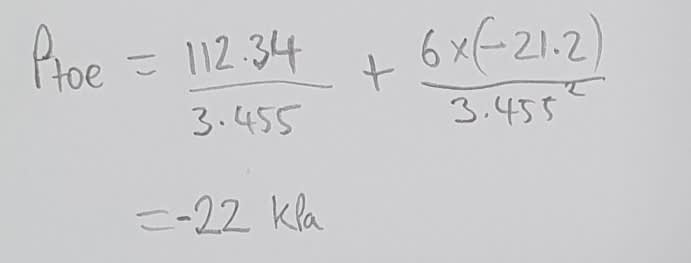Hi There,
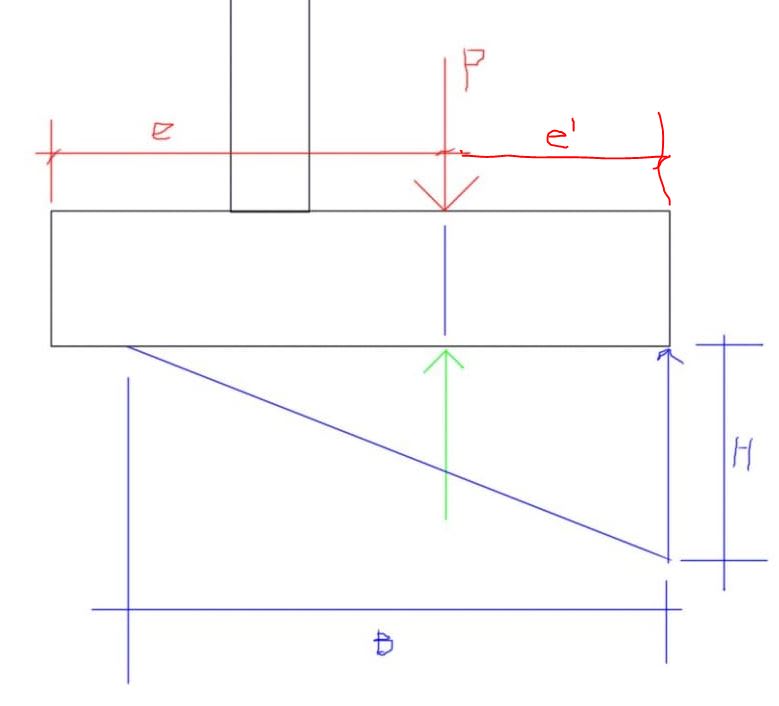
I am currently designing a retaining wall. The architect would like a 6’8” retaining wall, although the height of the embankment is 14’, which will require a sloped backfill.
As a result the foundation ended up being quite large, when considering the height of the wall. I am calculating the bearing pressure but am running into some calculations that are raising some questions and I would like to know whether I am going about this the right way?
I attached the calcs to this thread but I am getting a negative moment when taking moments about the centerline of the base.
I am getting a negative pressure at the toe and positive at the heel. The negative toe pressure would cause the heel pressure to increase higher than what I show in the calcs. What is the formula to calculate the accurate heel pressure?
Although the toe pressure is negative, I can only see that being realized in the heel pressure exceeds the allowable bearing capacity of the ground, which is unlikely.
The stability checks for the wall were fine for sliding and overturning.
Any help would be appreciated, as I am not sure if I went about these bearing pressure check cals the right way.
I am currently designing a retaining wall. The architect would like a 6’8” retaining wall, although the height of the embankment is 14’, which will require a sloped backfill.
As a result the foundation ended up being quite large, when considering the height of the wall. I am calculating the bearing pressure but am running into some calculations that are raising some questions and I would like to know whether I am going about this the right way?
I attached the calcs to this thread but I am getting a negative moment when taking moments about the centerline of the base.
I am getting a negative pressure at the toe and positive at the heel. The negative toe pressure would cause the heel pressure to increase higher than what I show in the calcs. What is the formula to calculate the accurate heel pressure?
Although the toe pressure is negative, I can only see that being realized in the heel pressure exceeds the allowable bearing capacity of the ground, which is unlikely.
The stability checks for the wall were fine for sliding and overturning.
Any help would be appreciated, as I am not sure if I went about these bearing pressure check cals the right way.