Shear Flow Thought Exercise

I think you would get full composite action, which would be almost identical to no composite action. The top flanges don't want to slide much and it wouldn't take many shear screws to keep them from sliding (assuming zero slip in screws). Although in reality, I think such miniscule slip that you are trying to prevent would happen anyway.

Have to be careful... development of shear by fasteners may be difficult.

Rather than think climate change and the corona virus as science, think of it as the wrath of God. Feel any better?

-Dik

Before doing that, I would look very carefully to see if there is an HSS adequate for the purpose without using an insertion.

If insertion is necessary, it would be best to fill the gap on the bottom with steel shims at the points of bearing (and further along the span if possible).

BA

I suspect the screws will be in tension rather than shear (at least mostly), and the effectiveness of the inner tube will be limited by the capacity of the screws near the end and the flexibility of the top flanges.

Assume the inner tube isn't subject to gravity, so it doesn't fall to sit on the the bottom flange. If the screws weren't there, the outer tube would push the inner tube as a rigid body down to the level of the midspan deflection (with no stress in the inner tube - it is just being pushed around). The screws however pull on the inner tube to clamp the two top flanges together. The details depend on the stiffness of the two tubes and screw spacing, but I suspect it will approximate a UDL on the inner tube through bearing and a tension reaction in the end screws or a few near the end - the deflected shapes need to match which means the moment diagrams need to match, thus the shear matches, thus the loads and reactions match - that's my thinking. If the flanges distort significantly, the load carried by the inner tube reduces because the overall deflection no longer needs to match - some of the rigid body movement of the inner tube can occur.

This leads to the packers at the supports as BAretired suggested, if the screws and flanges aren't up to the task (and good idea anyway).

The proposed section behavior will be composite ...but not sure how did you calculate the shear flow q..
Let us assume the tubes stitch welded to each other at two ends ... What will be the difference? Or,how higher will the resistance composite section than the superposition of the separate sections ?..

Thanks for the responses guys. Just to add some definition, this situation is common in the curtain wall industry. Aluminum mullions are reinforced with steel shapes. In the vast majority of cases the steel is shimmed tight within the depth of the mullion. This helps fabrication in addition to the engineering requirement. This question is less practical, and more about depth of understanding on a personal level.

I used the shear flow equation here:
My A' value is A of inner tube, and the y value is nearly 0. If the inner tube was replaced with a bar (ie. just the top flange of the tube), then the shear flow equation would give me intuitive results. However, I question the result in the double tube case since q is so low. Let's call the double tube condition Case A, and the bar only condition Case B.

@steveh49 I believe I was thinking along the same lines. In case A the tension in the fasteners could be assessed by considering the inner tube to be a simply supported beam. I would determine the UDL on that beam required to achieve the combined shape deflection that is anticipated in service. The reactions of the beam would then be the tension in the screws at the end of the inner tube...(maybe that is in-line with your explanation). Applying the same method to case B, the UDL to impose the service deflection would be VERY small, since the bar has minimal stiffness in isolation, but the value of q would be high since the NAs are no longer aligned. So in case B composite action is achieved by shear in the screws, and in case A composite action is achieved by tension.

Thinking with these extremes makes me wonder a) if I'm thinking about this correctly, and b) are there limitations of the typical shear flow I have ignored in the past? At what point do the fasteners see 30/70 shear/tension, 50/50, 70/30, etc...

I just did some basic models that indicate it works as I said, with the load applied to the inner tube approximately following the external load (UDL or concentrated load cases). There's a gremlin in the model to sort out as the inner tube moves slightly to one side (~0.1mm in a 1000mm span) even though the model is symmetrical as far as I can tell, otherwise I'd post some results.

I don't think fixing the tubes at the top alone results strictly in composite action as the shear flow at the level of the bottom face of the inner tube is zero, but is >zero in the web of the outer tube alongside the inner tube's flange, whereas the shear flow would be equal for a composite section (=VQ/I). This is load-sharing between non-composite members.

1) There is currently another, interesting, active thread here on shear flow that you might enjoy checking out: Link. It's the reason that you're seeing so much attention paid here to connector forces transverse to the member, particularly at the ends.

2) I believe that the shear flow equation that you've been attempting to apply is indeed applicable to the case of your thought experiment. That said, it's obviously not jiving with your intuition so, in a an effort to help with that, I'll attempt an intuitive response to the best of my ability:

INTUITIVE EXPLANATION

We structural engineers are basically students of Newtonian physics. As you'll recall with Newtonian physics, many sorts of things are conserved. Energy, mass, whatever... There's no such thing as a free lunch is one, somewhat pessimistic, interpretation of that conservation. Everything has a cost. But the reverse is also true in that, when you're only asking for, say, a fig newton and a box of apple juice, lunch is actually pretty cheap. The cost is commensurate with the benefit. Nature never asks that you over pay.

When we attempt to make two independent sections behave compositely:

1) The cost is how onerous the fastening requirement is and;

2) The benefit is the degree to which the composite moment of inertia is increased relative to the sum of the original, non-composite moments of inertia.

Looking at some extreme cases:

A) Where the two constituent members have their centroids on the same vertical axis, composite behavior yields no improvement at all with respect to the moment of inertia. The lunch tray is empty. Commensurately, the cost is zero with respect to horizontal shear connection demand.

B) Where one constituent member is stacked above the other, the composite moment of inertia is the maximum that it can be without introducing a physical separation between the two members. The lunch is hearty and nourishing. Commensurately, the cost is substantial in reflection of the benefit received.

In your hypothetical arrangement, the composite moment of inertial is only marginally more than the sum of the independent moments of inertial. Thus. you are closer to having an empty lunch tray and the horizontal shear demand is small.

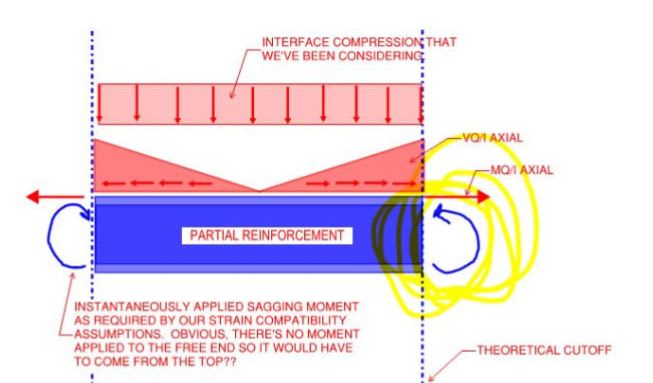
3) In that other thread that I referenced, we arrived at a fairly robust free body diagram of the the reinforcing piece considered there. The same model should apply quite well to the inner tube of your case. Note, in particular, that that composite action involves five actions imposed upon the reinforcing piece:

i) Distributed horizontal shear, VQ/I.

ii) A distributed, transverse load applied upon the reinforcing by the main member through the interface connection.

iii) A concentrated, transverse load applied upon the reinforcing by the main member at the the ends of the reinforcing and opposing [ii].

iv) Where the reinforcing does not extend the full length, a concentrated horizontal shear, MQ/I.

v) Where the reinforcing does not extend the full length, a concentrated moment at the ends of the reinforcing.

4) I've done a fair bit of curtain wall reinforcing design and these are my thoughts on how it should be done:

A) Recognize that almost nobody does this 100% correctly. Or even close.

B) If you've got the packing at the ends, you really don't have to worry about [iii] above.

C) For one wind direction, [ii] will be resolved by the main member pushing against the reinforcing and creating no axial demand in the fasteners (only the shear). For the other wind direction [ii] needs to be resolved by the member pulling away from the reinforcing and creating a tension demand in the fasteners which should be combined with the VQ/I shear demand.

D) Per AaronMcD, it's pretty common to assume that the two members are not composite owing to uncertainties regarding connection slip etc. At least that's the case when the benefit to the moment of inertia is quite modest as I discussed in [#2]. So design the fasteners for composite behavior but consider ignoring the composite action for the macroscopic design of the composite member.

An important observation related to the free body diagram above: the composite behavior is a result of more than just the horizontal shear, VQ/I action. Rather, it's two primary actions:

1) Horizontal shear, VQ/I and;

2) The transverse load acting across the member interface.

The greater the improvement to the composite moment of inertia, the larger the role of [VQ/I], relatively speaking; the smaller the improvement to the composite moment of inertia, the lager the role of the transverse load acting across the interface. In the extreme, there is no VQ/I and I_comp = I_main + I_reinf.

Disregard what I wrote earlier. I have forgotten the fundamentals. Gere & Timoshenko are giving me a refresher.

I would look to the loadpath out of the inner channel. Is the inner channel connected along the length of the beam (on the upper face) ? So the outer beam bears against the channel, which being stiff will resist downward deflection. I assume the channel is connected only to the beam, so it'd have to give the load that it picked up from the beam back to the beam, presumably at a place where the beam is as stiff (in bending) as the channel, ie close to the supports, as a tension load on these fasteners. I don't know if VQ/It will work, as you've got a redundant structure, where competing loadpaths depend on their relative stiffness.

another day in paradise, or is paradise one day closer ?