Eng-Tips is the largest engineering community on the Internet

Intelligent Work Forums for Engineering Professionals

Register Log in
  • Congratulations waross on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!

Bending moment/stress in bolt in double shear (with gap between plates) 2

Status
Not open for further replies.
enghelp2806

enghelp2806

Aerospace
Nov 16, 2020
16
US
Hi,

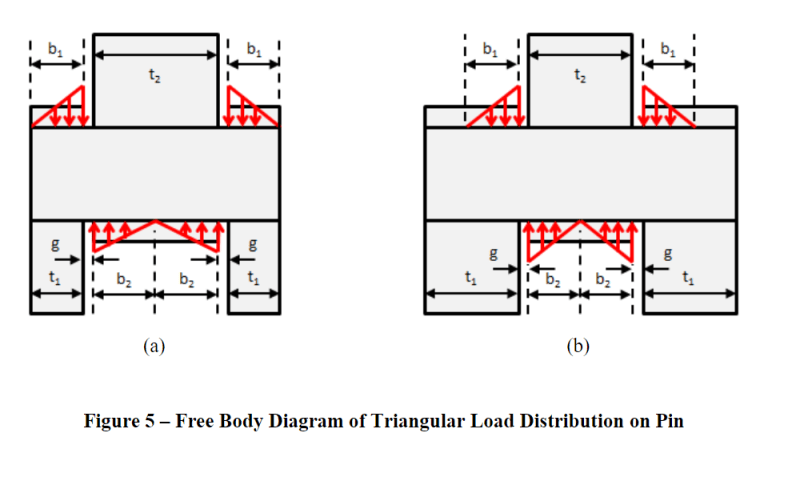
I'm trying to calculate the bending moment/stress in a bolt in double shear with a gap between the plates. I know there are much more realistic ways to do this, like assuming that the clevis (two outer plates) create bearing/contact stresses, the use of semiempirical formulas, or methods like the lifting lug (aircraft) method. I've been working in this aerospace industry for 5 years now, so these methods would be my preferred choice, but really I'm trying to simplify this as much as possible as this is for an undergraduate level course that I'm taking as graduate credit. The professor has asked us to think about this problem in the simplest terms so here goes.

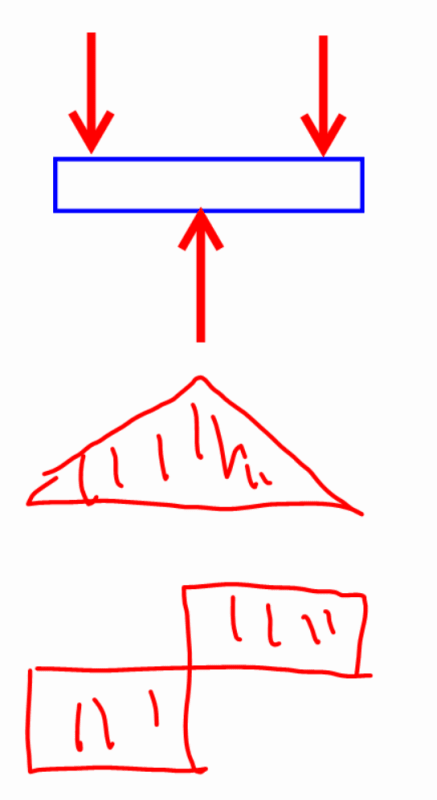
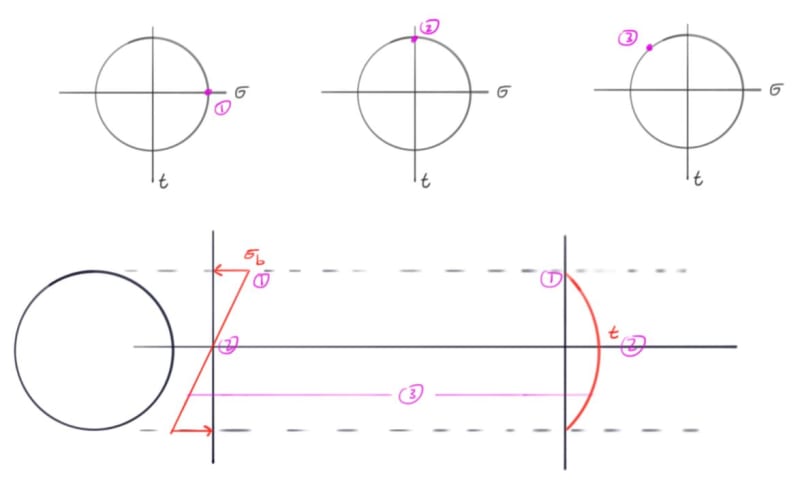
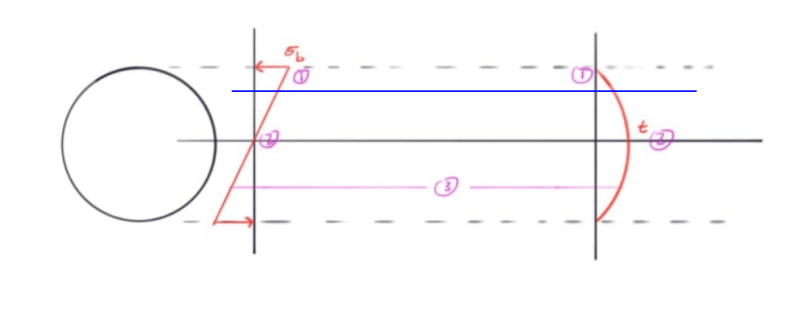
The shear stresses due to bending in this joint can be approximated as tau = VQ/Ib, but the professor has asked us to think about the bending stress. Would it make sense to assume this joint resembles a simply supported beam, with pin/roller supports at the two outer plates? If so, then the bending stress would simplify be sigma = Mc/I and be located at the center of the bolt.

Otherwise, I could assume the joint as a redundant beam fixed at both ends, where Mc/I still applies, but there would be moment reacted at the center and ends.

Thanks
 
Replies continue below

Recommended for you

Sort by date Sort by votes
My guess is that the professor is trying to prompt you to consider the interaction of bending and shear via something like a Von Mises check.

This thread should probably be moved to the student's forum even though you're only sort of a student.
 
Upvote 0 Downvote
You first need to make some assumptions about how the bolt is loaded by the plates:
- is there a head/nut on the bolt that reacts moments?
- what is the distribution of contact stress on the bolt shank? Uniform? Triangular thru plat thickness?
Draw a free body diagram.
 
Upvote 0 Downvote
the simplest model is a double cantilever, length = the distance between the mid-thickness planes on the clevis lugs. The gap increases the bending moment in the bolt.

There is no significant interaction between bending shear and shear stress ... why ?

another day in paradise, or is paradise one day closer ?
 
Upvote 0 Downvote
rb1957 said:
There is no significant interaction between bending shear and shear stress ... why ?
Click to expand...

The interaction that I spoke of was between the flexural stresses (local tension and compression) and the shear stresses. Classic Von Mises stuff as I mentioned previously: Link.
 
Upvote 0 Downvote
yep, and they don't interact ... where is peak bending ? where is peak shear ? what is the shear at peak bending ? what is the bending at peak shear ?

another day in paradise, or is paradise one day closer ?
 
Upvote 0 Downvote
rb1957 said:
yep, and they don't interact ... where is peak bending ? where is peak shear ? what is the shear at peak bending ? what is the bending at peak shear ?
Click to expand...

I'm fairly confident that they do interact. A clevis pin exhibits the two important things that you need for that:

1) As you yourself have mentioned, it's essentially a double cantilever. So high moments will exist alongside high shears near the center of the pin.

2) The nature of the cross section is such that bending and shear are not, predominantly, resisted in different parts of the cross section such as with a wide flange beam.
 
Upvote 0 Downvote
ok, I guess we have very different ideas about the bending and shear stress distributions in a pin.

another day in paradise, or is paradise one day closer ?
 
Upvote 0 Downvote
Perhaps. The first sketch below shows the model that I go to first. There are fancier ways to look at it, as shown in the second sketch, but I see little value in debating the merits of that until OP post's his own free body diagram, if he chooses to. My intent here was simply to point out one possible nuance that OP's professor might be trying to tease out of his students on this assignment. Obviously, I know no more about the assignment than OP has thus far shared.

What load distribution have you been assuming that would have no instances of significant shear simultaneously present with significant flexure?

c01_ey8klp.png


c02_zmwgll.png
 
Upvote 0 Downvote
yes, along the beam peak moment and peak shear happen at the same location, but on the cross section the two stresses don't interact, IMHO.

your approach for FBD for this problem is exactly mine.

another day in paradise, or is paradise one day closer ?
 
Upvote 0 Downvote
I believe rb1957 is referencing the internal stress state resulting from the shear and moments. Which I agree that the stresses don't interact but only at the locations of peak shear or peak bending stress at all other locations through the section depth the stresses do interact in the von-mise combination.

Capture_sykiw0.jpg


I'm making a thing: (It's no Kootware and it will probably break but it's alive!)
 
Upvote 0 Downvote
enghelp2806:
Check out APA Technical Report 12 it is geared towards wood but shows force distribution assumptions in the dowel fasteners: Link

I'm making a thing: (It's no Kootware and it will probably break but it's alive!)
 
Upvote 0 Downvote
Celt83 said:
Which I agree that the stresses don't interact but only at the locations of peak shear or peak bending stress at all other locations through the section depth the stresses do interact in the von-mise combination.
Click to expand...

Agreed. One would be concerned with the stresses at, say, the blue line shown below.

These two things will be true of pretty much any elastic section in:

1) Flexural stresses will be at a maximum at the extreme fibers.

2) Shear stresses will be zero at the extreme fibers.

Obviously, that cannot be taken to mean that we never have to worry about Von Mises stresses.

C01_pkygoq.png
 
Upvote 0 Downvote
Status
Not open for further replies.

Similar threads

Luceid
  • Question
Punching Shear in Foundations - Bending
Replies
11
Views
326
cliff234
cliff234
jcs284
  • Locked
  • Question
When to consider pin bending in double shear applications
Replies
2
Views
35
SWComposites
SWComposites
struct_eeyore
  • Locked
  • Question
One bolt double shear connection in lieu of 2-bolt AISC?
Replies
5
Views
59
canwesteng
canwesteng
doubtfulDeadLoad
  • Locked
  • Question
Opening in punching shear critical sections WITH SHEAR REINFORCEMENT
Replies
2
Views
84
doubtfulDeadLoad
doubtfulDeadLoad
Tstruct
  • Locked
  • Question
Propped cantilever bending moment
Replies
4
Views
84
TRAK.Structural
TRAK.Structural

Part and Inventory Search

Sponsor

Back
Top