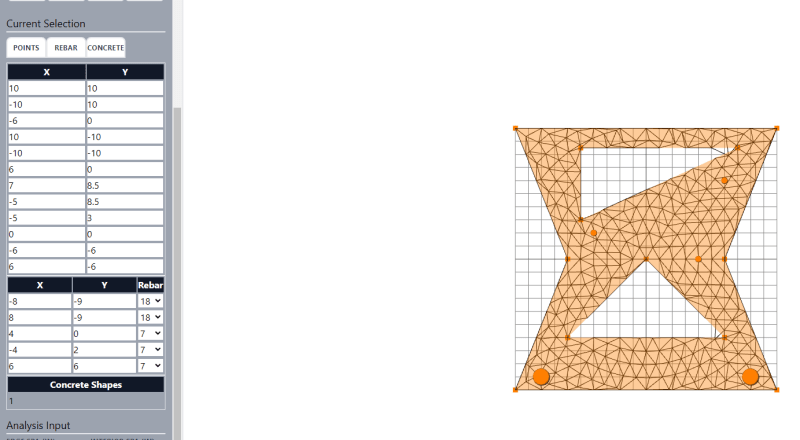sticksandtriangles
Structural
I am attempting to generate a concrete PM diagram tool and I am running into an odd bug, I am hoping someone can point me in the right direction.
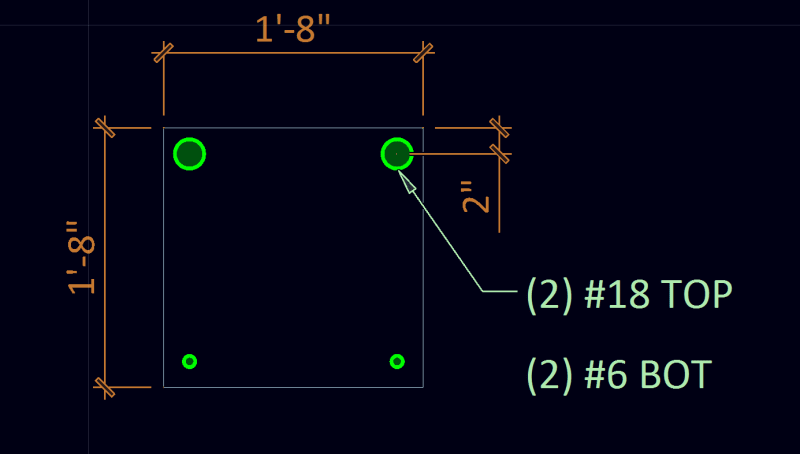
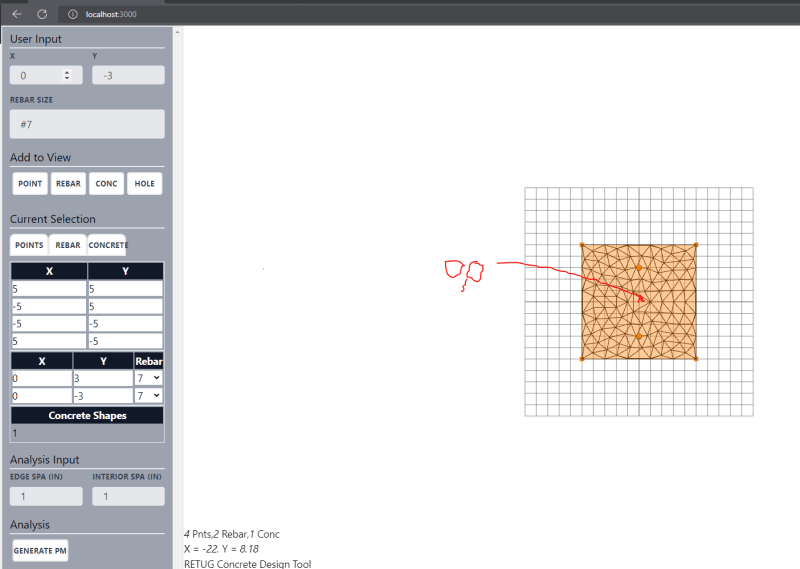
A quick summary of where I am at, I have tool that allows the user to place concrete shapes and rebar on the screen.
After the user input is collected, a mesh and assumed strain profiles are generated for the concrete shape and rebar.
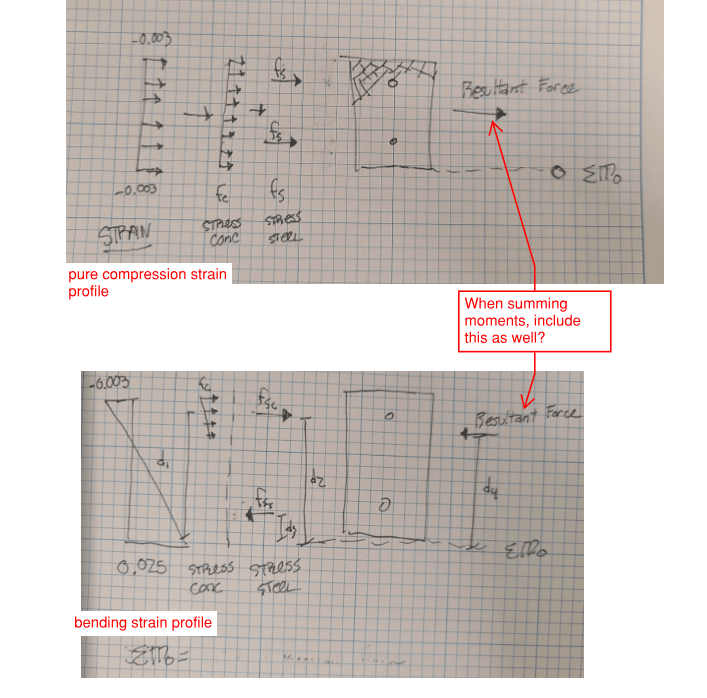
With the strain profiles and stress strain curves of the materials, I perform sum of forces in the vertical direction and sum of moments about the bending axis of interest.
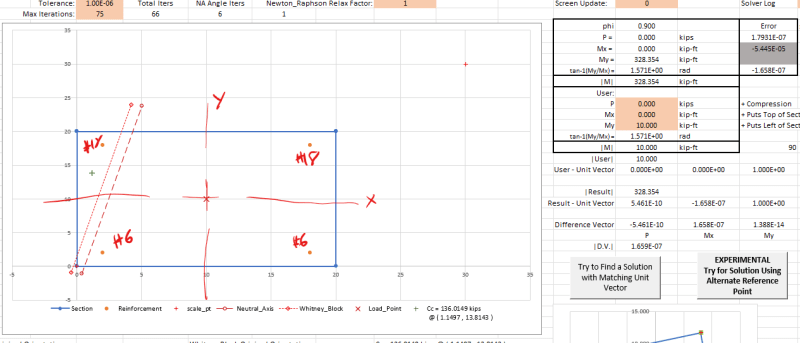
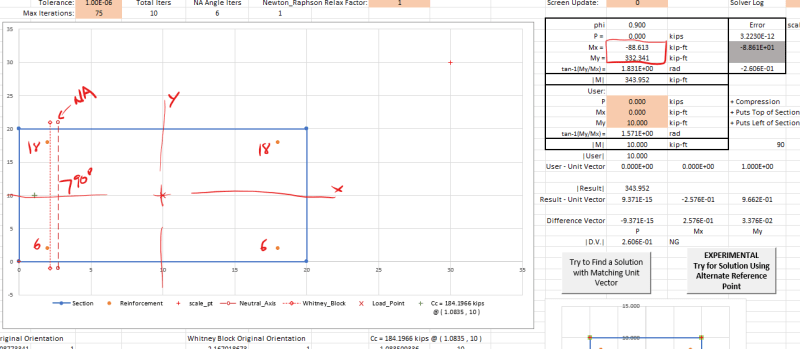
Where the trouble comes in, I get differing moment results depending on where the shape is generated.
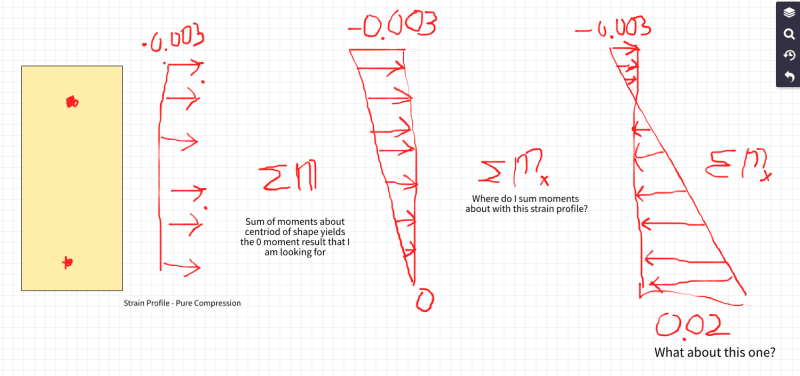
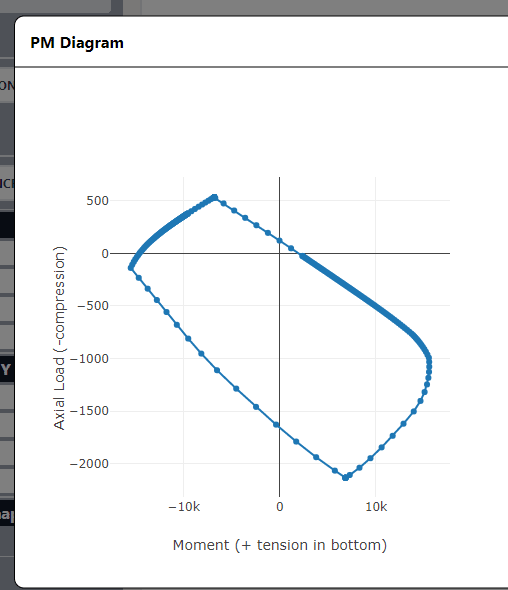
When the shape is generated with the center at 0, 0, I get the results I expect for a PM Diagram:
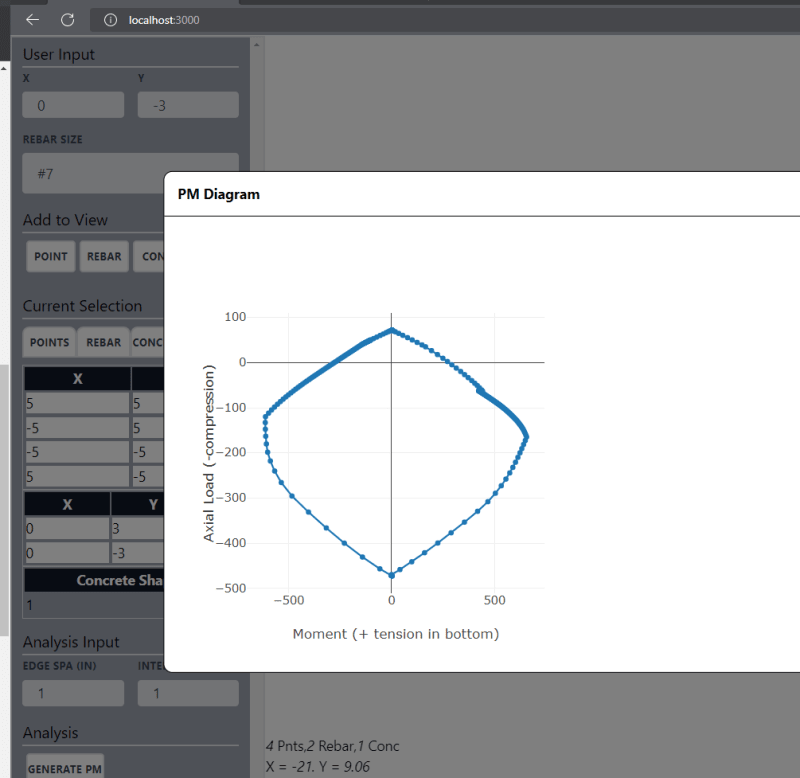
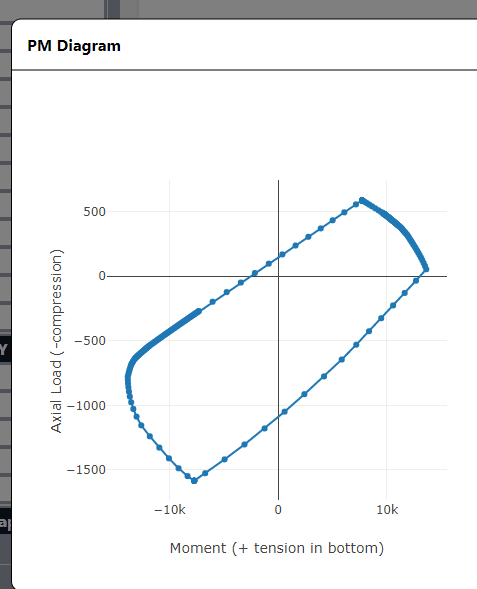
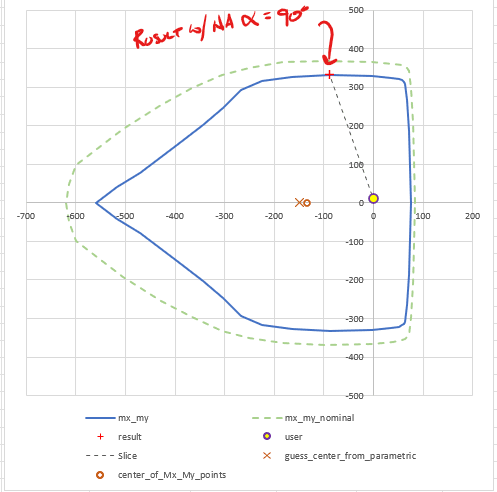
When the shape is generated with the center anywhere else, I get odd skewed moment results, but the same max tension and compression values:

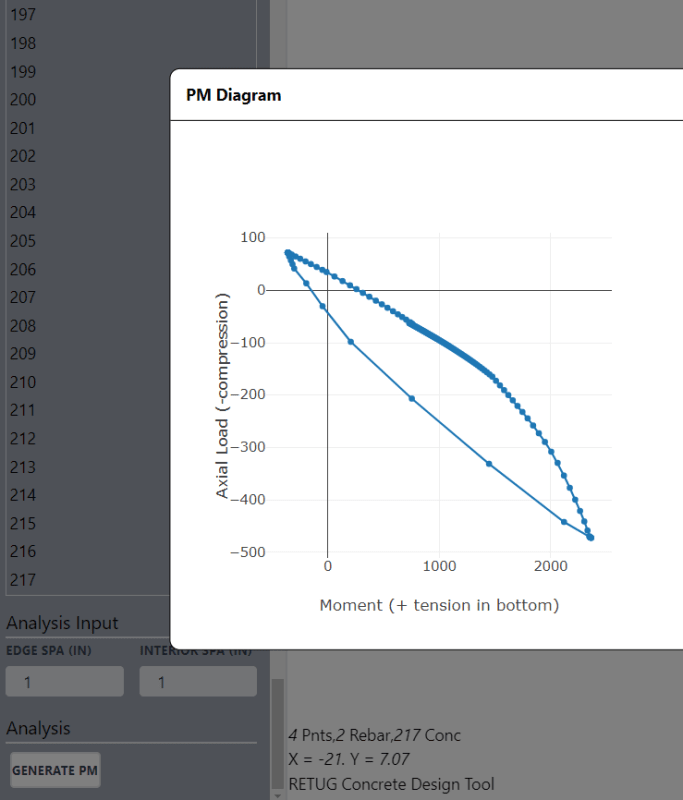
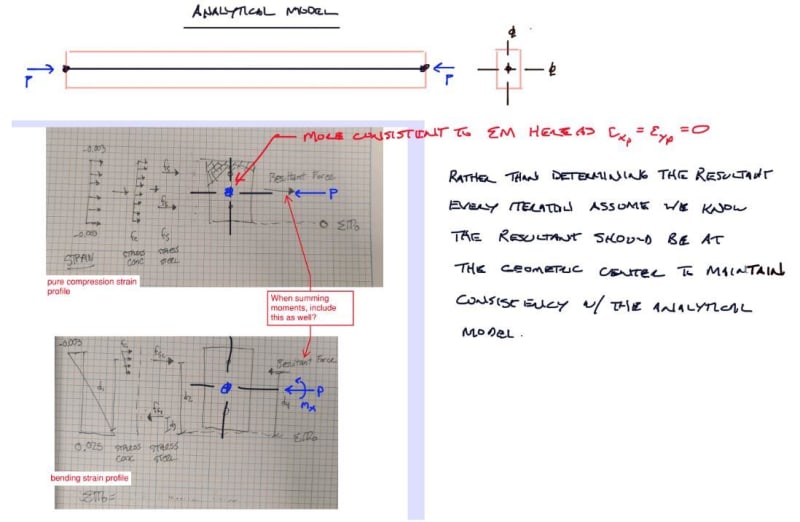
I think my problem lies in where I am summing my moments about (notice that the max tension and max compression values match between the two diagrams, just the moment values are off). What point should I be summing moments about for an arbitrary concrete PM calculation? I thought it could be any point, as long as it was the same point, but that clearly is not working.
I have the code up on github if interested.
Code of interest:
S&T -
A quick summary of where I am at, I have tool that allows the user to place concrete shapes and rebar on the screen.
After the user input is collected, a mesh and assumed strain profiles are generated for the concrete shape and rebar.
With the strain profiles and stress strain curves of the materials, I perform sum of forces in the vertical direction and sum of moments about the bending axis of interest.
Where the trouble comes in, I get differing moment results depending on where the shape is generated.
When the shape is generated with the center at 0, 0, I get the results I expect for a PM Diagram:


When the shape is generated with the center anywhere else, I get odd skewed moment results, but the same max tension and compression values:


I think my problem lies in where I am summing my moments about (notice that the max tension and max compression values match between the two diagrams, just the moment values are off). What point should I be summing moments about for an arbitrary concrete PM calculation? I thought it could be any point, as long as it was the same point, but that clearly is not working.
I have the code up on github if interested.
Code of interest:
JavaScript:
//looping through each stress strain profile
for (var strainProfile of strainProfiles) {
let concForce = 0
var steelForce = 0
var concMoment = 0
var steelMoment = 0
for (var concEle of concElements) {
concForce += concMaterial.stress(strainFunction(strainProfile[0],concEle.centriod.y, strainProfile[1]))*concEle.area
//concMoment += -concMaterial.stress(strainFunction(strainProfile[0],concEle.centriod.y, strainProfile[1]))*(concEle.area*concEle.centriod.y-strainProfile[1])
//concMoment += -concMaterial.stress(strainFunction(strainProfile[0],concEle.centriod.y, strainProfile[1]))*(concEle.area)*(concEle.centriod.y-concCentriod[1])
concMoment += -concMaterial.stress(strainFunction(strainProfile[0],concEle.centriod.y, strainProfile[1]))*(concEle.area)*(concEle.centriod.y-strainProfile[1])
}
for (var steelRebar of rebarShapes) {
//area times stress(strain)
// this has been updated
steelForce += Math.PI/4*(rebarDia[steelRebar.rebarSize])**2*steelMaterial.stress(strainFunction(strainProfile[0],steelRebar.geometry.attributes.position.array[1], strainProfile[1]))
steelMoment += -Math.PI/4*(rebarDia[steelRebar.rebarSize])**2*steelMaterial.stress(strainFunction(strainProfile[0],steelRebar.geometry.attributes.position.array[1], strainProfile[1]))*(steelRebar.geometry.attributes.position.array[1]-strainProfile[1])
}
totalForceArray.push(steelForce+concForce)
totalMomentArray.push(steelMoment+concMoment)
}
return [totalForceArray, totalMomentArray]
}S&T -