Burunduk
Mechanical
- May 2, 2019
- 2,577
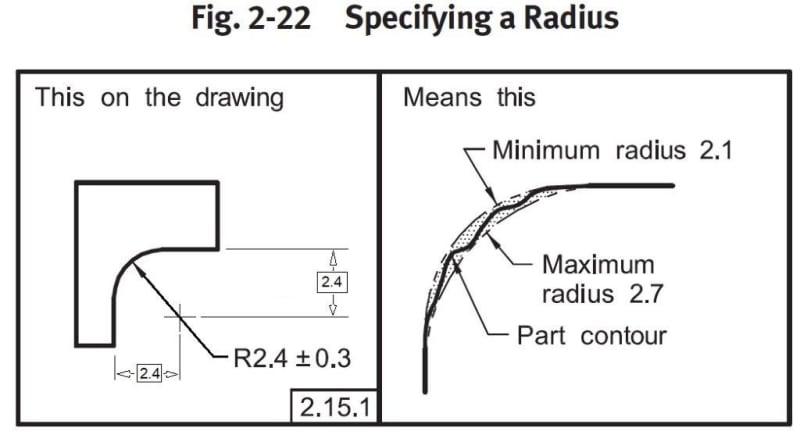
One of the changes from the 2009 to the 2018 version of Y14.5, is the interpretation of the tolerance zone of a radius dimension with a direct tolerance.
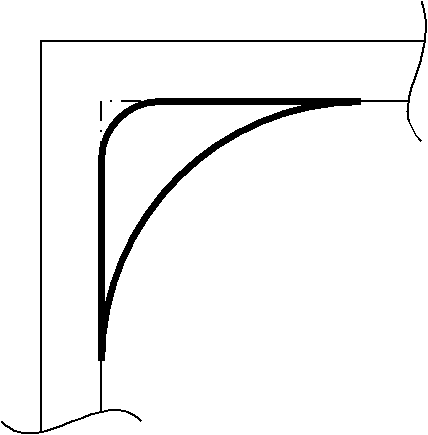
According to 5.16.1 (page 39), the problematic crescent shaped tolerance zone from the previous versions is still intact, but only when the center of the radius "is not located". The new thing is - "When the center of the radius is located via dimension(s), the arcs are concentric". No example is shown for the new definition.
Does anyone here know or understand the reasoning behind this change and how the new scheme with the located/dimensioned center is to be implemented correctly? Is the idea here to establish some sort of true center on which the tolerance zone arcs are based? If so, is this another case for basic dimensions unrelated to a geometric tolerance? Does this become sort of a profile tolerance that controls both the form and the location of the actual radius feature, only without explicit datum references? Alternatively, does it not control location and only change the shape of the tolerance zone? If so, would reference dimensions for center location be appropriate?
According to 5.16.1 (page 39), the problematic crescent shaped tolerance zone from the previous versions is still intact, but only when the center of the radius "is not located". The new thing is - "When the center of the radius is located via dimension(s), the arcs are concentric". No example is shown for the new definition.
Does anyone here know or understand the reasoning behind this change and how the new scheme with the located/dimensioned center is to be implemented correctly? Is the idea here to establish some sort of true center on which the tolerance zone arcs are based? If so, is this another case for basic dimensions unrelated to a geometric tolerance? Does this become sort of a profile tolerance that controls both the form and the location of the actual radius feature, only without explicit datum references? Alternatively, does it not control location and only change the shape of the tolerance zone? If so, would reference dimensions for center location be appropriate?