Hi
I was wondering if someone could help me explain a conundrum I'm having?
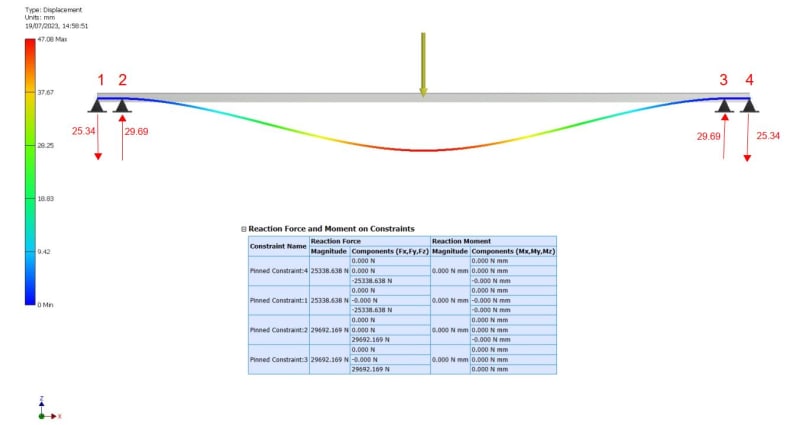
I have a steel section slung between to I beams with a load equally positioned in the center ( The I beams are 2.5m apart ) With a load of say 8kN on two constraints I get an equal division of the load including the beam weight. If I have two pinned constraints on each end of my beam, the reaction forces increase massively, one at 25kN and the end one at -29kN. How is this explained.
Thanks in advance
Dave
I was wondering if someone could help me explain a conundrum I'm having?
I have a steel section slung between to I beams with a load equally positioned in the center ( The I beams are 2.5m apart ) With a load of say 8kN on two constraints I get an equal division of the load including the beam weight. If I have two pinned constraints on each end of my beam, the reaction forces increase massively, one at 25kN and the end one at -29kN. How is this explained.
Thanks in advance
Dave