Continue to Site

Eng-Tips is the largest engineering community on the Internet

Intelligent Work Forums for Engineering Professionals

Register Log in
  • Congratulations KootK on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!

Lateral Bracing of Continuous Beams 1

Status
Not open for further replies.
KB4444

KB4444

Civil/Environmental
Nov 29, 2021
17
My question is with the lateral bracing requirements of a continuous beam under a uniformly distributed load.

For the image below the specific example I have has wall girts/roof purlins spanning (3) columns. The members will have sheeting on the outside that I am treating as a lateral support (attached every 1ft). The issue I have is that the moment of the girt changes from + to -; so does the sheeting only count as lateral torsional bracing for the + moment length of the beam (where the flange it's attached to is in compression)? Or is there a part of the code I'm missing that allows the bracing of one side of a continuous beam to count as laterally braced for the entire length?

I am lookin at this with respect to the Canadian code so CSA - S16.

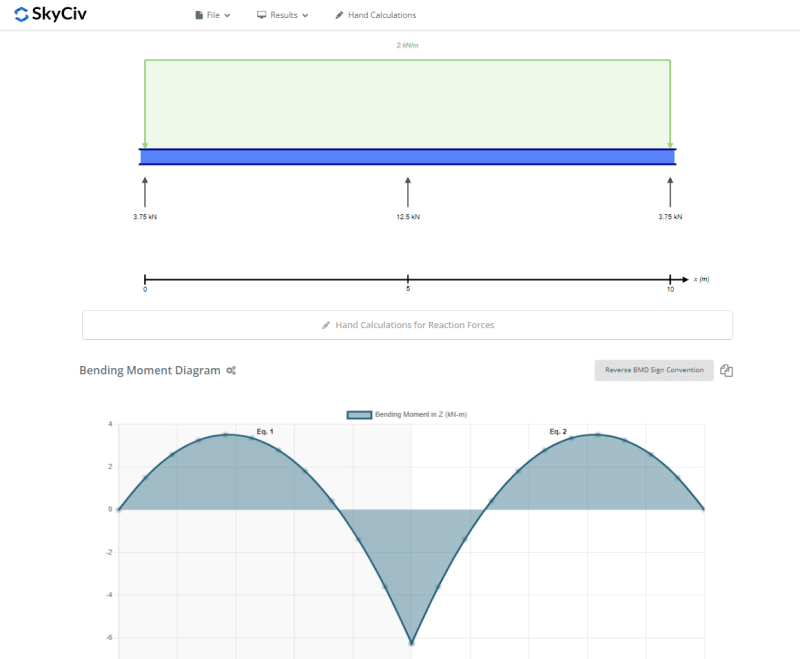
Screenshot_2023-10-10_155759_d1f91o.png
 
Replies continue below

Recommended for you

Sort by date Sort by votes
The bottom flange over the support is the compression flange, and is therefore subject to LTB over its unbraced length. In the AASHTO bridge design spec, anyway, the contraflexure point can be considered a braced point, so the unbraced length would be from there to where the bottom flange is braced by a diaphragm or cross-frame.
 
Upvote 0 Downvote
In the US AISC specification, the inflection point is NOT a brace point and the entire length must be considered unbraced...however, AISC has a factor (Cb) that is derived from moment values along the span and correctly calculates the moment capacity based on those values.

 
Upvote 0 Downvote
@BridgeSmith I am not familiar with AASHTO bridge spec, but I have read thru Yura bracing for stability before and from that article, point of inflection cannot be considered as bracing. I am not sure when the AASHTO publication came out, after or before Yura's article (1995). But it will be interesting to know which part of the AASHTO states that.
 
Upvote 0 Downvote
OP said:
Or is there a part of the code I'm missing that allows the bracing of one side of a continuous beam to count as laterally braced for the entire length?
Click to expand...

No, I don't think the bracing on the one side affects the bending capacity of the beam when it's other side is in compression. At least that's what the US codes have been saying for 20+ years. My thoughts on this:
a) The code seems clear that points of inflection cannot be used as "brace points" (as pointed out by BridgeSmith).
b) You can increase the moment capacity by the moment variation factor (Cb as pointed out by JAE) since it varies so much through the unbraced length.
c) I've seen people add small kicker braces to the opposite flange of the beam so that they can reduce the unbraced length. I've also seen people use full depth stiffeners at certain locations where one side is braced. The thinking being that if you restrain torsional deflection, then you can reduce the unbraced length as well.
 
Upvote 0 Downvote
You'll want to start by providing torsional restraint to your beam at the interior support which will point brace both flanges. If this doesn't get you a desirable beam size, start considering things like kicker bracing to the bottom flange at the mid spans etc.

Bracing the top flange does help to brace the bottom flange but the mechanics of that are tedious and not well suited to routine design. It's called constrained axis lateral torsional bucking. Only break the glass on that in cases of extreme desperation... or maybe if you have a killer spreadsheet already set up.
 
Upvote 0 Downvote
It seems I was confused, or thinking of the older methods:

AASHTO LRFD 9th Ed. Commentary said:
In past practice, points of contraflexure sometimes have been considered as brace points when the influence of moment gradient was not included in the lateral–torsional buckling resistance equations. In certain cases, this practice can lead to a substantially unconservative estimate of the flexural resistance. These Specifications do not intend for points of contraflexure to be considered as brace points. The influence of moment gradient may be accounted for correctly through the use of Cb and the effect of restraint from adjacent unbraced segments may be accounted for by using an effective length factor less than 1.0. Suggested values of Cb for compact web sections, subject to reverse curvature bending with no intermediate bracing or bracing on only one flange, are provided in Yura and Helwig (2010), and in the commentary to Article F1 of AISC (2016b).
Click to expand...

Mea Culpa.
 
Upvote 0 Downvote
Thanks for reporting back to clarify things Rod. I always like to know about what AASHTO has to say but rarely invest the time to look it up myself.
 
Upvote 0 Downvote
Status
Not open for further replies.

Similar threads

Eng868
  • Question
Lateral Torsional Bracing – Floor Voids
Replies
3
Views
522
Eng868
Eng868
kaffy
  • Question
Regarding Lateral Torsional Buckling Bracing 1
Replies
4
Views
263
KootK
KootK
Z
  • Question
Lateral X Bracing on bottom Truss Bridge
Replies
0
Views
357
zurlcorn
Z
kaffy
  • Question
Regarding Bracing for lateral torsional Buckling 1
Replies
2
Views
193
KootK
KootK
Deener
  • Question
Lateral Loading for Fall Arrest Gantry Beams 1
Replies
5
Views
989
Lomarandil
Lomarandil

Part and Inventory Search

Sponsor

Back
Top Bottom