a126z
Student
- Nov 26, 2023
- 36
1. In ABAQUS, for a three-dimensional cantilevered cylinder structure, there is only a force in the Y direction at the top of the free end, so why is there a branch reaction force in the X and Z directions at the solid end (with all six degrees of freedom constrained)?
2. The support reaction force is in equilibrium with the external force. But the external force is only Fy, so the support reaction force should only be Fy and Mx. In fact, the values of the support reaction forces Fx,Fz,My,Mz are not 0, why is this? I want a scientific and reasonable explanation.
3. I have turned off geometric nonlinearity and the material is linear. I have only defined the modulus of elasticity and Poisson's ratio. In addition, the structure is subjected to a force of 1E4 kN, even if I change it to 100 kN, the phenomenon is still the same.
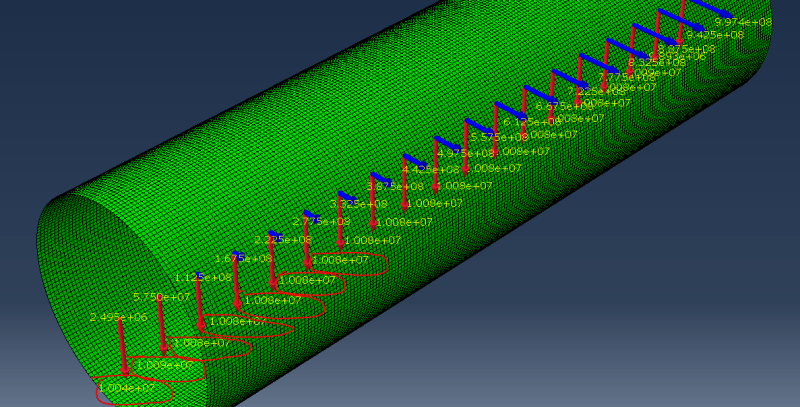
4. The following figure shows the resultant bearing reaction force calculated at 1E4kN with the model.

2. The support reaction force is in equilibrium with the external force. But the external force is only Fy, so the support reaction force should only be Fy and Mx. In fact, the values of the support reaction forces Fx,Fz,My,Mz are not 0, why is this? I want a scientific and reasonable explanation.
3. I have turned off geometric nonlinearity and the material is linear. I have only defined the modulus of elasticity and Poisson's ratio. In addition, the structure is subjected to a force of 1E4 kN, even if I change it to 100 kN, the phenomenon is still the same.
4. The following figure shows the resultant bearing reaction force calculated at 1E4kN with the model.