RevSol
Mechanical
- Feb 3, 2024
- 3
Howdy all.
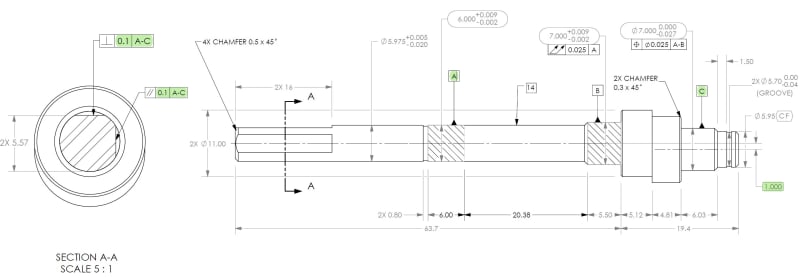
Would the following work to control the orientation of these flats to the 2 axial datums that are offset?
If I have datum A establishing 1 axis, datum C (eccentric portion) establishing the other axis.
Then referencing A-C as a common datum to establish clocking of the shaft and then use parallelism and perpendicularity to control the flats?
Or is there a better, cleaner, easier way? I need to know how to best clock this part to the eccentric portion.
Thanks!!!
Would the following work to control the orientation of these flats to the 2 axial datums that are offset?
If I have datum A establishing 1 axis, datum C (eccentric portion) establishing the other axis.
Then referencing A-C as a common datum to establish clocking of the shaft and then use parallelism and perpendicularity to control the flats?
Or is there a better, cleaner, easier way? I need to know how to best clock this part to the eccentric portion.
Thanks!!!

