MumtazDogan
Chemical
- Mar 29, 2024
- 6
Hello everyone,
I am really struggling when I try to deal with gaseous flows. For liquids, everything is really straightforward for me, the terms in the energy equation, applying Bernoulli's Equation or Energy Equation etc.
But when it comes to gases, I really start to struggle and can't describe the system and what is happening. I can approximate some gaseous systems with Bernoulli, but when it comes to General Equation of Energy, they seem to contradict and Energy Equation seem not intuitively to me.
The equation I am trying to use is this
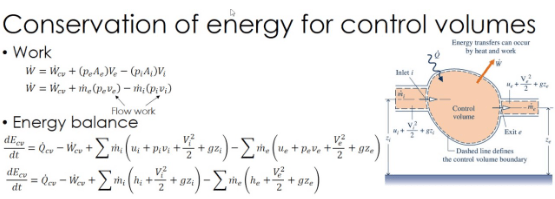
I always thought that the Bernoulli's Equation and head form of it was coming from the General Equation of Energy. But, the results seem not being interpreted the same.
Below, I have two questions, one is related with an atmospheric tank vent, the other is related with a gas flowing in a very long pipe whose radius is increasing to keep the linear velocity constant. I really do not understand how the terms in the General Equation of Energy changes in these situations.
1)

2)
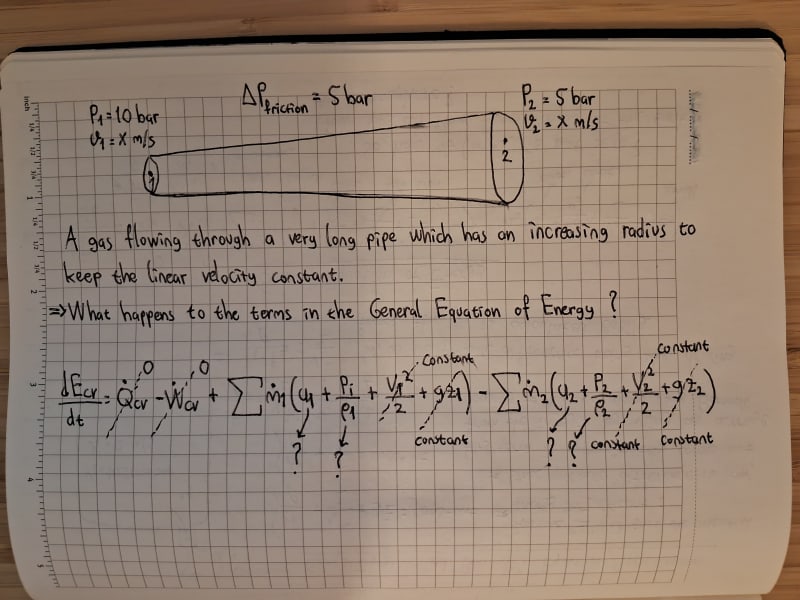
Thanks in advance.
I am really struggling when I try to deal with gaseous flows. For liquids, everything is really straightforward for me, the terms in the energy equation, applying Bernoulli's Equation or Energy Equation etc.
But when it comes to gases, I really start to struggle and can't describe the system and what is happening. I can approximate some gaseous systems with Bernoulli, but when it comes to General Equation of Energy, they seem to contradict and Energy Equation seem not intuitively to me.
The equation I am trying to use is this
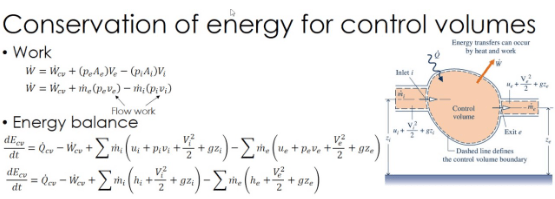
I always thought that the Bernoulli's Equation and head form of it was coming from the General Equation of Energy. But, the results seem not being interpreted the same.
Below, I have two questions, one is related with an atmospheric tank vent, the other is related with a gas flowing in a very long pipe whose radius is increasing to keep the linear velocity constant. I really do not understand how the terms in the General Equation of Energy changes in these situations.
1)

2)

Thanks in advance.


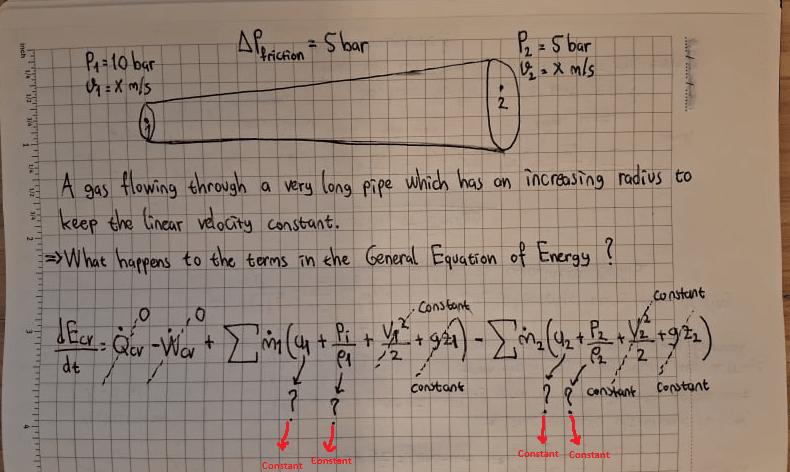
![[hourglass] [hourglass] [hourglass]](/data/assets/smilies/hourglass.gif)
![[atom] [atom] [atom]](/data/assets/smilies/atom.gif)