Tygra_1983
Student
Hi all
I have been learning the shooting method for boundary value problems. For second order differential equations, as you may well know, you need two initial conditions to get the procedure going; one known condition and one guess. I am using eulers method, so I am reducing the second order ODE to two first order ODE's. I am using a random equation to practice with that is in the form:
y'' = 4y' + 2y^3 + 2*x.
If z = y'
then
z' = y''
Which coverts to two first order ODE's
z' = 4z + 2y^3 + 2x
y' = z
My boundary conditions are y(0) = 0 and y(4) = 0. I am shooting the initial condition so that after 4 iterations my y value = 0.
So to break it down, I have made 4 guesses for z (the intial condition of the slope). These are -10, -2, 1 and 4. When I plug these into the code I get the corresponding values: -1.3405e+09, -1.0737e+07, 1348392 and 8.5814e+07. I figure these are enough points to get a good approximation using intepolation. Consequently to get my correct intial value of the slope so that at the end y(4) = 0, or close to zero.
Here is the result of my intepolation:
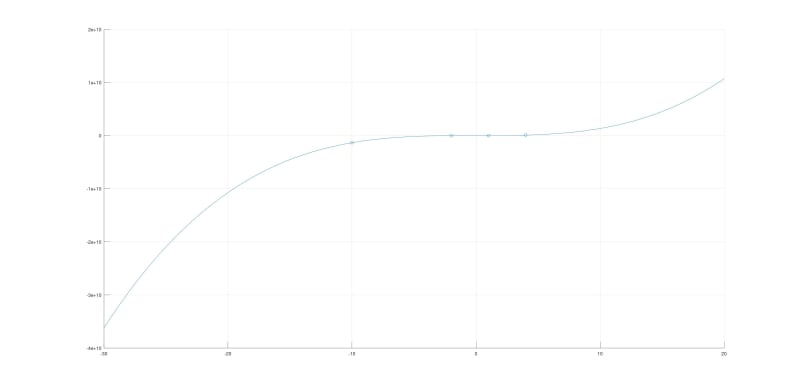
From the curve, the line crosses the x axis at -0.044486. This should be my value for the initial condition of the slope at z. However, when I perform the for loop again with this value I get a value of 428.3653. This is nowhere near zero.
I am doing all this in Octave. I don't expect anyone to go through the whole code, but its there so you can see what I'm doing.
I feel bad for posting such a long question, but I'm really stuck on why this method is not working. I hope someone can help please?
I have been learning the shooting method for boundary value problems. For second order differential equations, as you may well know, you need two initial conditions to get the procedure going; one known condition and one guess. I am using eulers method, so I am reducing the second order ODE to two first order ODE's. I am using a random equation to practice with that is in the form:
y'' = 4y' + 2y^3 + 2*x.
If z = y'
then
z' = y''
Which coverts to two first order ODE's
z' = 4z + 2y^3 + 2x
y' = z
My boundary conditions are y(0) = 0 and y(4) = 0. I am shooting the initial condition so that after 4 iterations my y value = 0.
So to break it down, I have made 4 guesses for z (the intial condition of the slope). These are -10, -2, 1 and 4. When I plug these into the code I get the corresponding values: -1.3405e+09, -1.0737e+07, 1348392 and 8.5814e+07. I figure these are enough points to get a good approximation using intepolation. Consequently to get my correct intial value of the slope so that at the end y(4) = 0, or close to zero.
Here is the result of my intepolation:

From the curve, the line crosses the x axis at -0.044486. This should be my value for the initial condition of the slope at z. However, when I perform the for loop again with this value I get a value of 428.3653. This is nowhere near zero.
I am doing all this in Octave. I don't expect anyone to go through the whole code, but its there so you can see what I'm doing.
I feel bad for posting such a long question, but I'm really stuck on why this method is not working. I hope someone can help please?
Code:
h=3
z = -10
x = 0
y = 0
for i = 1:4
z(i+1) = z(i) + (2*y(i)^3 + 4*z(i) + 2*x(i))*h;
y(i+1) = y(i) + z(i)*h
x(i+1) = x(i) + h;
end
q1 = y(end)
z = -2
x = 0
y = 0
for i = 1:4
z(i+1) = z(i) + (2*y(i)^3 + 4*z(i) + 2*x(i))*h;
y(i+1) = y(i) + z(i)*h
x(i+1) = x(i) + h;
end
q2 = y(end)
z = 1
y = 0
x = 0
for i = 1:4
z(i+1) = z(i) + (2*y(i)^3 + 4*z(i) + 2*x(i))*h;
y(i+1) = y(i) + z(i)*h
x(i+1) = x(i) + h;
end
q3 = y(end)
y = 0
x = 0
z = 4
for i = 1:4
z(i+1) = z(i) + (2*y(i)^3 + 4*z(i) + 2*x(i))*h;
y(i+1) = y(i) + z(i)*h
x(i+1) = x(i) + h;
end
q4 = y(end)
p1 = [-10, q1]
p2 = [-2, q2]
p3 = [1, q3]
p4 = [4,q4]
P = [p1;p2;p3;p4]
X = [1 (-10) (-10)^2 (-10)^3;
1 (-2) (-2)^2 (-2)^3;
1 1 1^2 1^3;
1 (4) (4)^2 (4)^3 ]
A = inv(X)*P(:,2)
x = -30:0.1:20;
y = A(1) + A(2).*x + A(3).*x.^2 + A(4).*x.^3;
scatter(P(:,1),P(:,2))
hold on
plot(x,y)
grid on
grid on
y1 = interp1(y,x,0,'spline')
z = y1
y =0
x = 0
for i = 1:4
z(i+1) = z(i) + (2*y(i)^3 + 4*z(i) + 2*x(i))*h;
y(i+1) = y(i) + z(i)*h
x(i+1) = x(i) + h;
end