Jungyong Ko
Mechanical
Hi all,
I need help calculating the diameter of a bar with a groove, as shown in the attached diagram. I am designing a coupler to connect a valve and an actuator following ISO 5211.
I want to find out the shear stress based on the torque that passes through the coupler. However, the cross-section of the coupler is not a simple circle or rectangle but a shape with a cut-out in the middle, which makes the calculation difficult.
Because I don't know how to calculate the shear stress, I also can't find the correct diameter.
Can someone explain how to calculate the shear stress or diameter for this shape? Any methods or resources would be very helpful.
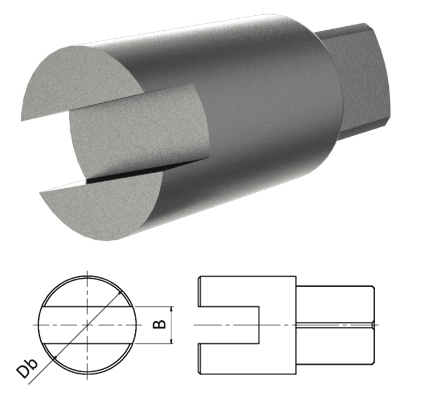
I need help calculating the diameter of a bar with a groove, as shown in the attached diagram. I am designing a coupler to connect a valve and an actuator following ISO 5211.
I want to find out the shear stress based on the torque that passes through the coupler. However, the cross-section of the coupler is not a simple circle or rectangle but a shape with a cut-out in the middle, which makes the calculation difficult.
Because I don't know how to calculate the shear stress, I also can't find the correct diameter.
Can someone explain how to calculate the shear stress or diameter for this shape? Any methods or resources would be very helpful.


