I am wondering if anyone here has ever rationalized the snow drift loading on a structure where the roof transitions into a pyramid or cone shape. For example, a flat roof with a large steel structure skylight. Here is a rough sketch of what the cross section of the roof would be:
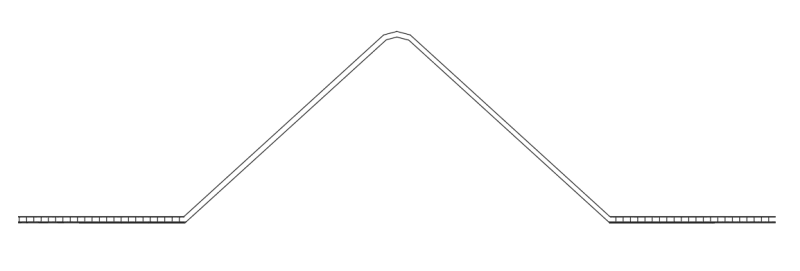
The slope of this structure is at a 1:1, 7.6m above top of roof.
Under the NBCC2020 code I am trying to determine which snow loadings would be applicable.
Straight off the bat there will be sliding, which is easily addressible.
Some other considerations would be to take it as a roof projection (obstruction) or treating it as a high-low condition, both of which come with reasons why they may not be applicable.
Starting with roof projections:
[ul]
[li]The roof is at a 45° so it may not really be a projection, but wind will still push a drift up to it[/li]
[li]The perimeter of this upper-roof structure is ~62m so the drift length can be very long depending what you take l0 to be[/li]
[li]Since the roof is at a 45°, what would the appropriate projection height be? As we increase projection height, the drift increases, until eventually height stops governing.[/li]
[li]Roof projections don't address the source area the same way high-low does, but given that we are including sliding seperately should be okay[/li]
[/ul]
Now if we treat it as a high-low:
[ul]
[li]There is no clear "h" difference in height, but case 2 of Figure 4.1.6.5.-B addresses the condition where wind pushes snow up to our "upper roof" which ends up governing anyways[/li]
[li]The snow load value treating it as a high low is lower than a projection, but still quite high.[/li]
[/ul]
To give some context, when running it as a roof projection, with 31m l0 representing half of the perimeter, I get a 14kPa drift that is 20m long. If i take l0 as 20m (the diameter of my cone shape) its a 10kPa drift thats 16m long. Both of these are assuming the height is 7m since that is the height from top of roof to the peak of this structure, because I can't rationalize an appropriate height to take as alluded to above.
If ran as a high-low condition, the case 2 yields much more reasonable results of 5.8kPa of 6m length, assuming the source area is the area of my cone roof.
Neither of the values above include sliding, which would be added to them. Sliding would have a greater influence on my shorter drifts as the code indicates to distribute the sliding snow over the length xd.

The slope of this structure is at a 1:1, 7.6m above top of roof.
Under the NBCC2020 code I am trying to determine which snow loadings would be applicable.
Straight off the bat there will be sliding, which is easily addressible.
Some other considerations would be to take it as a roof projection (obstruction) or treating it as a high-low condition, both of which come with reasons why they may not be applicable.
Starting with roof projections:
[ul]
[li]The roof is at a 45° so it may not really be a projection, but wind will still push a drift up to it[/li]
[li]The perimeter of this upper-roof structure is ~62m so the drift length can be very long depending what you take l0 to be[/li]
[li]Since the roof is at a 45°, what would the appropriate projection height be? As we increase projection height, the drift increases, until eventually height stops governing.[/li]
[li]Roof projections don't address the source area the same way high-low does, but given that we are including sliding seperately should be okay[/li]
[/ul]
Now if we treat it as a high-low:
[ul]
[li]There is no clear "h" difference in height, but case 2 of Figure 4.1.6.5.-B addresses the condition where wind pushes snow up to our "upper roof" which ends up governing anyways[/li]
[li]The snow load value treating it as a high low is lower than a projection, but still quite high.[/li]
[/ul]
To give some context, when running it as a roof projection, with 31m l0 representing half of the perimeter, I get a 14kPa drift that is 20m long. If i take l0 as 20m (the diameter of my cone shape) its a 10kPa drift thats 16m long. Both of these are assuming the height is 7m since that is the height from top of roof to the peak of this structure, because I can't rationalize an appropriate height to take as alluded to above.
If ran as a high-low condition, the case 2 yields much more reasonable results of 5.8kPa of 6m length, assuming the source area is the area of my cone roof.
Neither of the values above include sliding, which would be added to them. Sliding would have a greater influence on my shorter drifts as the code indicates to distribute the sliding snow over the length xd.

