Henrique Orlandini
Mechanical
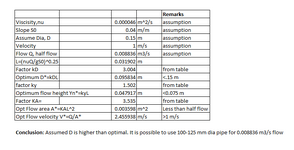
Hello again. I'm working on a spreadsheet to aid my coworkers in sizing a Lube Oil System as per API 614 6th editions, and one of the requirements is that all gravity return oil lines must be at most half full.
So, what I've been trying to do is to determine what is the flow that could run through an exactly half full pipe. I tried looking first into Manning's formula first, but it doesn't sit well with lubricating oil due to the vastly different viscosities of water and oil. Then I tried to look into Darcy-Weisbach formula, but I couldn't also get a solution because the friction factor for laminar flow depends on the Reynolds number and the Reynolds number depends on the flow, which is what I'm trying to determine. Going into iterative or analytical solutions isn't feasible either because I need to put this on an Excel spreadsheet.
Basically, I need some light on those scenarios:
So, what I've been trying to do is to determine what is the flow that could run through an exactly half full pipe. I tried looking first into Manning's formula first, but it doesn't sit well with lubricating oil due to the vastly different viscosities of water and oil. Then I tried to look into Darcy-Weisbach formula, but I couldn't also get a solution because the friction factor for laminar flow depends on the Reynolds number and the Reynolds number depends on the flow, which is what I'm trying to determine. Going into iterative or analytical solutions isn't feasible either because I need to put this on an Excel spreadsheet.
Basically, I need some light on those scenarios:
- Scenario 1: the pipe dimensions are known; it's a gravity return oil line (no pressure other than ATM) and the wetted area is set to 50% (half full pipe). Is there a way to determine the flow through that area?
- Scenario 2: the pipe dimensions are known; it's a gravity return oil line (no pressure other than ATM) and the flowrate is also known. Is there a way to determine the wetted area?